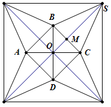
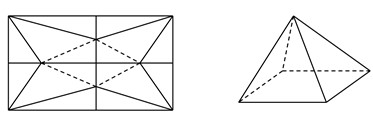
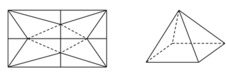
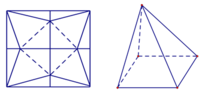
Trong một cuộc thi làm đồ dùng học tập do trường phát động, bạn An nhờ bố làm một hình chóp tứ giác đều bằng cách lấy một mảnh tôn hình vuông ABCD có cạnh bằng 5cm, cắt mảnh tôn theo các tam cân AEB, CGD, DHA; sau đó gò các tam giác AEH, BEF, CFG, DGH sao cho bốn đỉnh A, B, C, D trùng nhau tạo thành khối chóp tứ giác đều. Thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng:
A. 4 10 3 .
B. 4 10 5 .
C. 8 10 3 .
D. 8 10 5 .
Đáp án A.
Gọi cạnh đáy của khối chóp là x với
0 < x < 5 2 2 .
Chiều cao của khối chóp là
h = 5 2 2 − x 2 2 − x 2 2 = 25 − 5 x 2 2 .
Vậy thể tích của khối chóp là
V = 1 3 . h . S = 1 3 . x 2 . 25 − 5 x 2 2 = 1 3 25 x 4 − 5 x 5 2 2 .
Xét hàm số f x = 25 x 4 − 5 x 5 2 trên 0 ; 5 2 2 ,
ta có f ' x = 100 x 3 − 25 x 4 2 = 0 ⇔ x = 2 2 .
Suy ra giá trị lớn nhất của thể tích là V = 1 3 . f 2 2 2 = 4 10 3 .