Chọn B.
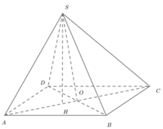
Phương pháp: Mấu chốt bài toán là chỉ ra được tam giác SAC vuông tại S.
Cách giải: Gọi O là giao điểm của AC và BD, H là hình chiếu của S lên mặt đáy.


Chọn B.

Phương pháp: Mấu chốt bài toán là chỉ ra được tam giác SAC vuông tại S.
Cách giải: Gọi O là giao điểm của AC và BD, H là hình chiếu của S lên mặt đáy.


Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 600. Tính thể tích của khối chóp S.ABCD theo a
A. a 3 6 6
B. a 3 3 6
C. a 3 6 12
D. a 3 6 2
Cho hình chóp đều S.ABCD có cạnh đáy bằng a , góc giữa cạnh bên và mặt đáy bằng 60 0 . Tính thể tích của khối chóp S.ABCD theo a .
A. a 3 6 6
B. a 3 6 2
C. a 3 6 12
D. a 3 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA=a 3 . Tính thể tích V của khối chóp S.ABCD
A. V= 3 a 3
B. V= 3 3 a 3
C. V= a 3
D. V=1/3 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA=a. Tính theo a thể tích V của khối chóp S.ABCD.
A. V = a 3
B. V = 1 6 a 3
C. V = 1 2 a 3
D. V = 1 3 a 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều, S C = S D = a 3 . Tính thể tích V của khối chóp S.ABCD theo a.
A. V = a 3 2 6 .
B. V = a 3 6 .
C. V = a 3 2 .
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều, SC = SD = a 3 . Tính thể tích V của khối chóp S.ABCD theo a
A. V = a 3 2 6
B. V = a 3 6
C. V = a 3 2
D. V = a 3 3 3
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy là a và cạnh bên là 2a. Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABCD
A. 16 a 3 π 14 49
B. 64 a 3 π 14 49
C. 64 a 3 π 14 147
D. 2 a 3 π 14 7
Cho khối chóp tam giác đều S.ABCD có cạnh đáy bằng a , S A = 3 . Tính thể tích V của khối chóp S.ABCD
A. V = 35 a 3 24
B. V = 3 a 3 6
C. V = 2 a 3 6
D. V = 2 a 3 2
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60 ° . Tính theo a thể tích khối chóp S.ABCD
A. V = a 3 6 6
B. V = a 3 6 2
C. V = a 3 6 3
D. V = a 3 3