Đáp án D
Tứ diện đều có 6 mặt phẳng đối xứng
Hình chóp tứ giác đều có 4 mặt phẳng đối xứng
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng
Hình hộp chữ nhật có 3 mặt phẳng đối xứng
Đáp án D
Tứ diện đều có 6 mặt phẳng đối xứng
Hình chóp tứ giác đều có 4 mặt phẳng đối xứng
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng
Hình hộp chữ nhật có 3 mặt phẳng đối xứng
Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều (như hình vẽ). Gọi V 1 ; V 2 lần lượt là thể tích của lăng trụ tứ giác đều và lăng trụ tam giác đều. So sánh V 1 và V 2
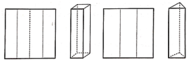
A. V 1 > V 2
B. V 1 = V 2
C. V 1 < V 2
D. Không so sánh được
Cho hình chóp tứ giác đều S.ABCD, đuờng cao SO. Biết rằng trong các thiết diện của hình chóp cắt bởi các mặt phẳng chứa SO, thiết diện có diện tích lớn nhất là tam giác đều cạnh bằng a, tính thể tích khối chóp đã cho
A. a 3 2 6
B. a 3 3 12
C. a 3 3 4
D. a 3 3 6
Cho lăng trụ lục giác đều A B C D E F . A ' B ' C ' D ' E ' F ' . Hỏi có bao nhiêu hình chóp tứ giác có 5 đỉnh là đỉnh của lăng trụ?
A. 492
B. 200
C. 360
D. 510
Cắt ba góc của một tam giác đều cạnh a các đoạn bằng x , 0 < x < a 2 phần còn lại là một tam giác đều bên ngoài là các hình chữ nhật, rồi gấp các hình chữ nhật lại tạo thành khối lăng trụ tam giác đều như hình vẽ. Tìm độ dài x để thể tích khối lăng trụ lớn nhất.
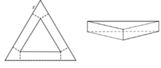
A. x = a 3
B. x = a 4
C. x = a 5
D. x = a 6
Cho hình lăng trụ tứ giác đều có các cạnh đều bằng a. Thể tích khối lăng trụ đều là
A. 2 a 3 2 3
B. a 3
C. 2 a 3 3
D. a 3 3 4
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, biết A ' A = A ' B = A ' C = 4 a . Hình chóp A’.ABC có tất cả bao nhiêu mặt phẳng đối xứng?
A. 3
B. Không có
C. 4
D. 2
Cho hình lăng trụ tứ giác đều, cạnh đáy bằng a, cạnh bên bằng b. Diện tích toàn phần của hình lăng trụ là
A. S t p = 2 a 2 + 4 a b .
B. S t p = 2 a 2 + 16 a b .
C. S t p = a 2 + 4 a b .
D. S t p = a 2 + 16 a b .
Từ một mảnh giấy hình vuông cạnh a , người ta gấp thành hình lăng trụ theo hai cách sau:
- Cách 1. Gấp thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều có thể tích là V 1 (Hình 1).
- Cách 2. Gấp thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều có thể tích là V 2 (Hình 2).
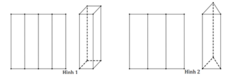
Tính tỉ số k = V 1 V 2
A. k = 3 3 8
B. k = 3 3 2
C. k = 4 3 9
D. k = 3 3 4
Cho hình lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác đều cạnh a. Góc giữa đường thẳng A'B' và mặt phẳng (A'B'C') bằng 45°. Diện tích mặt cầu ngoại tiếp tứ diện AB'C'C là:
A. 7 πa 2 3
B. C. .
C. 7 πa 2 6
D. 7 πa 2 9