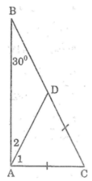
Xét ΔABC, ta có: ∠A= 90o; ∠B= 30o

Trên cạnh BC lấy điểm D sao cho CD = AC

Ta có: ΔACD cân tại C

Mà ∠C + ∠B = 90o (tính chất tam giác vuông)

Suy ra: ∠C = 90o - ∠B = 90o - 30o = 60o

Suy ra: ΔACD đều

Suy ra: AC = AD = DC và ∠A1= 60o

Ta có: ∠A1+ ∠A2 = ∠BAC = 90o

⇒ ∠A2 = 90o - ∠A1 = 90o - 60o = 30o

Trong ΔADB, ta có: ∠A2 = ∠B= 30o

Suy ra: ΔADB cân tại D (vì có 2 góc kề cạnh AB bằng nhau)

Hay AD = DB

Suy ra: AC = CD = DB mà CD + DB = BC

Vậy AC = 1/2 BC.

Bạn tự vẽ hình nhé

a) Xét tam giác ABC vuông tại A có B=30^o

Trên tia đối của tia AClấy điểm D sao cho AD=AC.

Xét tan giácABD và tam giác ABC có:

△ABC vuông tại A

△ABD vuông tại A

AB là cạnh chung.

AD=AC

Nên △ABC=△ABD (2 cạnh góc vuông)

=>góc ABD=góc ABC=30^o=>BDC=60^o

=>BD=BC=>△BDC cân tại B

mà góc BDC=60^o=>△BDC đều

=>DC=BC

Mà AC=\(\dfrac{1}{2}\)DC=>AC=\(\dfrac{1}{2}\)BC

*Cách khác: 

Gọi M là trung điểm của BC

Ta có: ΔABC vuông tại A(gt)

mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)

nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)

mà \(BM=CM=\dfrac{BC}{2}\)(M là trung điểm của BC)

nên AM=BM=CM

Xét ΔMAB có MA=MB(cmt)

nên ΔMAB cân tại M(Định nghĩa tam giác cân)

Xét ΔMAB cân tại M có \(\widehat{B}=60^0\)(gt)

nên ΔMAB đều(Dấu hiệu nhận biết tam giác đều)

Suy ra: AB=AM

mà \(AM=\dfrac{BC}{2}\)(cmt)

nên \(AB=\dfrac{BC}{2}\)(đpcm)

a)Gọi M là trung điểm cạnh huyền BC, Góc B=30 độ => Góc C=60 độ
Theo t/c đường trung tuyến trong tam giác vuông : AM=1/2.BC=MC
=> Tam giác AMC cân tại A
Mà góc C=60 độ => tâm giác AMC đều => AC=MC=1/2.BC => Cạnh đối diện với góc 30 độ bằng một nửa cạnh huyền

b)Theo t/c đường trung tuyến trong tam giác vuông : AM=1/2.BC=MC
Mà AC=BC => Tam giác AMC đều => Góc C=60 độ => Góc A=30 độ =>góc đối diện với cạnh bằng 1/2 cạnh huyền bằng 30 độ

Chứng minh: 

Ta có: ^C= 30° => ^B= 60° 
Trên cạnh BC lấy điểm M sao cho AB = BM. 
=> ∆ABM cân tại B mà ^B= 60° 
=>∆ABM đều 
=> AB= BM= AM (1) 
và ^BAM= ^B= ^BMA= 60° 
∆ABC vuông tại A 
=> ^B + ^C = 90° 
=> 60° + ^C = 90° 
=> ^C = 30° (2) 
Ta lại có : ^BAM + ^MAC = ^BAC 
=> 60° + ^MAC = 90° 
=> ^MAC = 30° (3) 
Từ (1) và (2): => ^MAC = ^C ( = 30°) 
=> ∆AMC cân tại M 
=> AM = MC (4) 
Từ (1) và (4): => AB = BM =mc 
=> 2AB = BM + MC 
=> 2AB = BC 
=> AB = BC/2 (đpcm)

b) 

Ví dụ tam giác ABC vuông tại A
trên cạnh BC lấyđiểm D sao cho AB=AD
mà tam giác ABC có góc A =90 độ
giả dụ góc C = 30 độ
thì góc B=60 độ
mà AB=BD
=>tam giác ABD là tam giác đều
=>góc BAD =60 độ
=>góc DAC=30 độ
mà góc C cũng = 30 độ
=>tam giác ADC cân tại D
=>AD=DC
có AB=BD=AD
=>D là trung điểm của BC
=> bạn tự kết luận