Tính số đo x trong mỗi hình 62, 63, 64:
Những câu hỏi liên quan
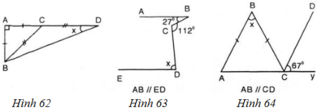
Tính số đo \(x\) trong mỗi hình 62, 63, 64 ?
62 x 63 + 75
_____________
12 + 62 x 64
\(\dfrac{62.63+75}{12+62.64}=\dfrac{62.63+63+12}{12+62.64}=\dfrac{62.64+12}{12+62.64}=1\)
Đúng 0
Bình luận (1)
\(\dfrac{62\times63+75}{12+62\times64}=\dfrac{62\times\left(64-1\right)+63+12}{12+62\times64}=\dfrac{62\times64-62+63+12}{12+62\times64}=\dfrac{62\times64+1+12}{12+62\times64}=1\)
Đúng 0
Bình luận (0)
Tính giá trị các lũy thừa sau: 62, 63, 64
62 = 6.6 = 36;
63 = 62.6 = 36.6 = 216;
64 = 63.6 = 216.6 = 1296.
Đúng 0
Bình luận (0)
Tính nhanh
a) (45-63+18) x (1+2+3+4+5+6+7+8+9)
b) 60-61+62-63+64-65+66-67+68-69+70
a. (45-63+18) x (1+2+3+4+5+6+7+8+9)
= 0 x (1+2+3+4+5+6+7+8+9) = 0
b. 60-61+62-63+64-65+66-67+68-69+70
= 60 + (-61-69)+(62+68)+(-63-67)+(64+66)-65+70
= 60 + (-130)+130+(-130)+130-65-70
= 60 + (-130+130) + (-130+130)-65+70
= 60 - 65 + 70 = 65
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính: 1 + 1/2 + 1/3 + ... + 1/62 + 1/63 + 1/64
E=125(1+62+63+64+...+62021)
chứng minh E +25 là số chính phương
Sửa lại đề một chút là \(E=125\left(1+6+6^2+6^3+...+6^{2021}\right)\) nhé.
Xét biểu thức \(P=1+6+6^2+6^3+...+6^{2021}\)
\(\Rightarrow6P=6+6^2+6^3+6^4+...+6^{2022}\)
\(\Rightarrow5P=6P-P=6^{2022}-1\) \(\Rightarrow P=\dfrac{6^{2022}-1}{5}\)
Vậy \(E=125P=25\left(6^{2022}-1\right)\) \(=25.6^{2022}-25\)
\(\Rightarrow E+25=25.6^{2022}=\left(5.6^{1011}\right)^2\) là số chính phương.
Đúng 2
Bình luận (0)
Cho A = 6 + 62 + 63 + 64 +....+ 62020
Tìm số tự nhiên n sao cho 6n = 5A + 6
A = 6 + 62 + 63 + 64 +....+ 62020
6A = 62 + 63 + 64 + 65 +....+ 62021
⇒ 6A - A = ( 62 + 63 + 64 +....+ 62021 ) - ( 62 + 63 + 64 +....+ 62020 )
⇒ 5A = 62021 - 6
Ta có: 6n = 5A + 6
⇔ 6n = 62021 - 6 + 6
⇔ 6n = 62021
⇔ n = 2021
Đúng 1
Bình luận (0)
\(\frac{x+1}{64}+\frac{x+2}{63}=\frac{x+3}{62}+\frac{x+4}{61}\)
X64=x63+x62+x^61+......+x2+x+2=0 Giải phương nghiệm nguyên