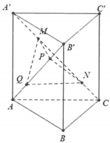
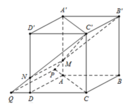
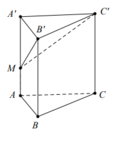
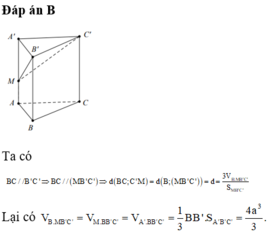
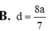Cho hình lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông cân tại C với CA = CB = a. Trên đường chéo CA' lấy hai điểm M, N. Trên đường chéo AB' lấy được hai điểm P, Q sao cho MPNQ tạo thành một tứ diện đều. Tính thể tích khối lăng trụ ABC. A’B’C’
A. 2 a 3
B. a 3 6
C. a 3
D. a 3 2