Tìm tập nghiệm của bất phương trình 3 x ≥ 5 - 2 x
A. [ 2 ; + ∞ )
B. 1 ; + ∞
C. [ 1 ; + ∞ )
D. [ 0 ; + ∞ )
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Tìm tập nghiệm của bất phương trình:
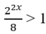
A. x > 3/2 B. x < 3/2
B. x > 2/3 D. x < 2/3
Tìm tập nghiệm của bất phương trình: 2 2 x 8 > 1
A. x > 3/2 B. x < 3/2
C. x > 2/3 D. x < 2/3
Tìm tập nghiệm của các bất phương trình sau: x + x < 2 x + 3 x - 1
Ta có: x + x < ( 2 x + 3 ) ( x - 1 )
Điều kiện: x ≥ 0
⇔ x + x < 2 x - 2 x + 3 x - 3
⇔ - x < - 3 ⇔ x > 3
Kết hợp điều kiện, tập nghiệm bất phương trình là: x > 3
Tìm tập nghiệm của các bất phương trình sau: ( x - 3 ) ( x - 2 ) ≥ 0
Ta có: x − 3 x − 2 ≥ 0
Điều kiện: x ≥ 2
Bất phương trình tương đương là x − 3 ≥ 0 x − 2 = 0 ⇔ x ≥ 3 x = 2
Vậy tập nghiệm của bất phương trình là S = { 2 } ∪ [3;+ ∞ )
Tìm tập nghiệm của các bất phương trình sau: ( x - 3 ) ( x - 2 ) ≥ 0
Ta có: ( x - 3 ) ( x - 2 ) ≥ 0
Điều kiện: x ≥ 2
Bất phương trình tương đương là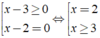
Vậy tập nghiệm của bất phương trình là x = 2 hoặc x ≥ 3
Tìm tập nghiệm của bất phương trình
(x^2 - 3x - 5) / (x^2 - 36). > = 1
đk: \(x\ne\pm6\)
Ta có: \(\frac{x^2-3x-5}{x^2-36}\ge1\)
\(\Leftrightarrow\frac{x^2-3x-5}{x^2-36}-1\ge0\)
\(\Leftrightarrow\frac{x^2-3x-5-x^2+36}{x^2-36}\ge0\)
\(\Leftrightarrow\frac{-3x+31}{x^2-36}\ge0\)
Xét 2 TH sau:
TH1: \(\hept{\begin{cases}-3x+31\ge0\\x^2-36>0\end{cases}}\) \(\Rightarrow x\le\frac{31}{3}\) và \(\orbr{\begin{cases}x>6\\x< -6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\frac{31}{3}\ge x>6\\x< -6\end{cases}}\)
TH2: \(\hept{\begin{cases}-3x+31\le0\\x^2-36< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge\frac{31}{3}\\-6< x< 6\end{cases}}\) => Vô lý
Vậy tập nghiệm phương trình \(\orbr{\begin{cases}\frac{31}{3}\ge x>6\\x< -6\end{cases}}\)
Bài 3 :Cho bất phương trình : 3x(2x + 5) x(6x -1) + 4
a) Giải bất phương trình và biểu diễn tập nghiệm trên trục số.
b) Tìm nghiệm nguyên nhỏnhất của bất phương trình trên.
1) Tìm tập nghiệm S của bất phương trình | 2x+1| > x+1
2) Tìm tất cả giá trị của tham số m để bất phương trình -x^2+x-m>0 vô nghiệm
2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
Giải các phương trình sau : 2 4x – 2 a) 2x - 3 = 5 b) (x + 2)(3x - 15) 0 z +1 I - 2 (x+ 1) (2 – 2) Câu 2: (2 điểm) số a) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục 2x + 2 <2+ 3 b) Tìm x để giá trị của biểu thức 3x - 4 nhỏ hơn giá trị của biểu thức 5x - 6
1:
a: 2x-3=5
=>2x=8
=>x=4
b: (x+2)(3x-15)=0
=>(x-5)(x+2)=0
=>x=5 hoặc x=-2
2:
b: 3x-4<5x-6
=>-2x<-2
=>x>1