Cho hình chóp S. ABC có S A ⊥ ( A B C ) , S A = a 3 . Tam giác ABC vuông cân tại B, AC = 2a. Thể tích khối chóp S. ABC bằng.
A. a 3 3
B. a 3 3 6
C. a 3 3 2
D. a 3 3 3
Những câu hỏi liên quan
cho hình chóp S. ABC có đáy ABC là tam giác vuông tại b, AB=a, BC=a√3 .Hình chiếu vuông góc của S lên mặt phẳng đáy là trung điểm H của AC, Sb=a√2Tisnh
a) d(B, (SAC))
b) d(C, (SBH))
c) d(H, (SBC))
Xem chi tiết
Kẻ \(BK\perp AC\Rightarrow BK\perp\left(SAC\right)\)
\(\Rightarrow BK=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow BK=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Kẻ \(CP\perp BH\Rightarrow CP\perp\left(SBH\right)\)
\(\Rightarrow CP=d\left(C;\left(SBH\right)\right)\)
\(\widehat{CBP}=\widehat{ACB}=30^0\Rightarrow CH=BC.sin30^0=\dfrac{a\sqrt{3}}{2}\)
\(BH=\dfrac{AC}{2}=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)\(\Rightarrow SH=\sqrt{SB^2-BH^2}=a\)
Kẻ \(HE\perp BC\) , kẻ \(HF\perp SE\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)
\(HE=CH.sin30^0=\dfrac{a}{2}\)
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{5}}{5}\)
Đúng 0
Bình luận (0)
Cho hình chóp S. ABC có đáy ABC là tam giác vuông cân tại B. Biết AB BC
a
3
,
S
A
B
^
S
B
C
^
90
0
và khoảng cách từ A đến mặt phẳng (SBC) bằng
a
2
Tính d...
Đọc tiếp
Cho hình chóp S. ABC có đáy ABC là tam giác vuông cân tại B. Biết AB = BC = a 3 , S A B ^ = S B C ^ = 90 0 và khoảng cách từ A đến mặt phẳng (SBC) bằng a 2 Tính diện tích mặt cầu ngoại tiếp hình chóp S. ABC.
A. 16 πa 2
B. 12 πa 2
C. 8 πa 2
D. 2 πa 2
Cho hình chóp S. ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S S trên đáy là điểm H nằm trên cạnh AC sao cho
A
H
2
3
A
C
, mặt phẳng (SBC) tạo với đáy một góc
60
0
.Tính thể tích khối chóp S. ABC A.
a
3
3...
Đọc tiếp
Cho hình chóp S. ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S S trên đáy là điểm H nằm trên cạnh AC sao cho A H = 2 3 A C , mặt phẳng (SBC) tạo với đáy một góc 60 0 .Tính thể tích khối chóp S. ABC
A. a 3 3 12
B. a 3 3 36
C. a 3 3 24
D. a 3 3 8
Cho hình chóp S. ABC có đáy là tam giác đều cạnh bằng a , cạnh bên SB vuông góc với mặt phẳng (ABC), SB 2a Tính thể tích khối chóp S. ABC. A.
a
3
4
B.
a
3
3
6
C.
3
a
3...
Đọc tiếp
Cho hình chóp S. ABC có đáy là tam giác đều cạnh bằng a , cạnh bên SB vuông góc với mặt phẳng (ABC), SB = 2a Tính thể tích khối chóp S. ABC.
A. a 3 4
B. a 3 3 6
C. 3 a 3 4
D. a 3 3 2
Cho hình chóp tam giác đều S. ABC cạnh đáy bằng a và cạnh bên bằng b. Tính thể tích khối chóp S. ABCD. A.
a
2
3
b
2
-
a
2
4
B. ...
Đọc tiếp
Cho hình chóp tam giác đều S. ABC cạnh đáy bằng a và cạnh bên bằng b. Tính thể tích khối chóp S. ABCD.
A. a 2 3 b 2 - a 2 4
B. a 2 3 b 2 - a 2 2
C. a 2 3 b 2 - a 2 6
D. a 2 3 b 2 - a 2 12
Cho hình chóp S. ABC có tam giác ABC có góc A bằng
120
0
và BC 2a. Tính bán kính mặt cầu ngoại tiếp hình chóp theo a. A.
a
3
2
B.
2
a
3
3
C.
a
6...
Đọc tiếp
Cho hình chóp S. ABC có tam giác ABC có góc A bằng 120 0 và BC = 2a. Tính bán kính mặt cầu ngoại tiếp hình chóp theo a.
A. a 3 2
B. 2 a 3 3
C. a 6 6
D. a 6 2
cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a góc abc=60• .SA vuông góc với mặt phẳng đáy. Tính:
a) d(A; (SBD))
b) d(C; (SAB))
Xem chi tiết
Đề thiếu dữ liệu để xác định độ dài SA rồi bạn
Đúng 0
Bình luận (0)
Cho hình chóp .S ABC có SA vuông góc mặt phẳng (ABC) tam giác ABC vuông tại .B Biết SA 2a, AB a, BC a
3
.Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho A. a B. 2a C. a
2
D. 2a
2
Đọc tiếp
Cho hình chóp .S ABC có SA vuông góc mặt phẳng (ABC) tam giác ABC vuông tại .B Biết SA= 2a, AB= a, BC= a 3 .Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho
A. a
B. 2a
C. a 2
D. 2a 2
Đáp án C
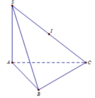
Gọi I là trung điểm của SC.
Khi đó I là tâm mặt cầu ngoại tiếp hình chóp
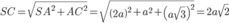Bán kính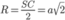 
Đúng 0
Bình luận (0)
Cho hình chóp S. ABC, đáy ABC là tam giác đều có độ dài cạnh bằng a, SA vuông góc với đáy,
S
A
a
3
. Tính thể tích V của khối chóp S. ABC A.
V
a
3
2
B.
V
3
a...
Đọc tiếp
Cho hình chóp S. ABC, đáy ABC là tam giác đều có độ dài cạnh bằng a, SA vuông góc với đáy, S A = a 3 . Tính thể tích V của khối chóp S. ABC
A. V = a 3 2
B. V = 3 a 3 4
C. V = a 3 12
D. V = a 3 4
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a
A
B
C
^
60
0
, cạnh bên SA vuông góc với đáy SA
a
3
Tính thể tích của khối chóp S. ABCD A.
a
3
4
B.
a...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a A B C ^ = 60 0 , cạnh bên SA vuông góc với đáy SA = a 3 Tính thể tích của khối chóp S. ABCD
A. a 3 4
B. a 3 3 6
C. a 3 2
D. a 3 3 3
