Tìm m để đồ thị hàm số y = x 4 - 2 m 2 x 2 + 1 có ba cực trị tạo thành tam giác vuông
A. m = ± 1
B. m = ± 2
C. m = 3
D. Đáp án khác
Tìm m để đồ thị hàm số y = x 4 - 2 m 2 x 2 + 1 có ba cực trị tạo thành tam giác vuông
A. m = ± 1
B. m = ± 2
C. m = 3
D. Đáp án khác
Cho hàm số bậc ba y=f(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y=|f(x)+m| có ba điểm cực trị là:
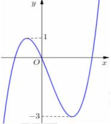
A. m ≤ - 1 hoặc m ≥ 3
B. m ≤ - 3 hoặc m ≥ 1
C. m = -1 hoặc m = 3
D. 1 ≤ m ≤ 3
Cho hàm số y = x 4 2 - 2 m 2 x 2 + 2 . Tìm tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng 64 15 là
![]()
![]()
tìm các giá trị thực của tham số m để đồ thị hàm số Cm : y= -x3 + 3mx2 - 2m3 có 2 điểm cực trị A, B sao cho đường thằng AB vuông góc với đường thằng d : y= -2x
Cho hàm số: y=(m-1)x+m (d)
a, Tìm m để hàm số đồng biến, nghịch biến
b, Tìm m để hàm số song song với trục hoành
c, Tìm m để đồ thị hàm số đi qua điểm A(-1;1)
d, Tìm m để đồ thị hàm số song song với đường thẳng có phương trrình: x-2y=1
e, Tìm m để đồ thị hàm số cắt trục hoành tại điểm A có hoành độ \(x=2-\frac{\sqrt{3}}{2}\)
f, Chứng minh rằng đường thẳng (d) luôn đi qua điểm cố định khi m thay đổi
Cho hàm số y = - x 3 + 3 x 2 + m (m là tham số) có đồ thị (C). Gọi A, B là các điểm cực trị của đồ thị (C). Khi đó, số giá trị của tham số m để diện tích tam giác OAB (O là gốc tọa độ) bằng 1 là:
A. 0
B. 2
C. 1
D. 3
Cho hàm số bậc nhất y= (a+2)x-a+1 có đồ thị là đường thẳng (d) a) Tìm a để hàm số nghịch biến trên R; b) Tìm a để đường thẳng (d) đi qua điểm M(-1,-4)
Lời giải:
a. Để hàm số nghịch biến trên R thì:
$a+2<0$
$\Leftrightarrow a< -2$
b.
Để $(d)$ đi qua $M(-1;-4)$ thì:
$y_M=(a+2)x_M-a+1$
$\Leftrightarrow -4=(a+2)(-1)-a+1$
$\Leftrightarrow a=\frac{3}{2}$
cho hàm số y=(m-1)x 4 (m là tham số, m khác 1) cso đồ thị là đường thẳng (d)
a)t tìm m để đường thẳng (d) song song với đường thẳng y=2x-3 . Hãy vẽ đồ thị hà số với giá trị m vừa tìm được
b) tìm m để khoảng cách từ gốc tòa độ đến đường thẳng (d) bằng 2
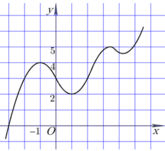
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương trình
f
(
x
2
-
2
x
)
=
m
có đúng 4 nghiệm thực phân biệt thuộc đoạn
[
-
3
2
;
7
2
]
.
A. 1
B. 4
C. 2
D. 3