Cho tam giác ABC có góc B=\(72^0\)các tia phân giác của góc A và C cát nhau tại K.Tính góc AKC.

Những câu hỏi liên quan
Cho tam giác ABC có góc B = 72 độ. Các tia phân giác của góc A và C cắt nhau tại H. Tính góc AKC
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC).Các tia phân giác của BAH và góc C cắt nhau ở K.Tính AKC?
Cho tam giác ABC có góc B = 72 độ. Các tia phân giác của các góc A và C cắt nhau ở K. Tính góc AKC
1.Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC)
a) Tìm các cặp góc phụ nhau
b) Tìm các cặp góc nhọn bằng nhau
2. Cho tam giác ABC có B^=72*. Các tia phân giác của các góc A và C cắt nhau ở K. Tính AKC^
a) Các cặp góc phụ nhau là:
góc BAH - góc HAC
góc BAH - góc ABH
góc ABH - góc ACB
góc HAC - góc ACB
b) Các cặp góc bằng nhau là:
góc BAH - góc HCA
góc ABH - góc HAC
góc AHB = góc AHC = góc BAC
Đúng 0
Bình luận (0)
Góc A + góc C = 1800 - góc B = 1080
AK là phân giác góc A
=> góc KAC = 1/2 góc A
CK là phân giác góc C
=> góc KCA = 1/2 góc C
suy ra: góc KAC + góc KCA = 1/2 (góc A + góc C)
=> góc KAC + góc KCA = 54
=> góc AKC = 1800 - (góc KAC + góc KCA) = 1260
Đúng 0
Bình luận (0)
Cho tam giác ABC có B = 72 độ . Các tia phân giác của các góc A và C cắt nhau ở k
a) Tính AkC
b) Vẽ tia Am là phân giác góc ngoài tại A. Cắt Ck tại n
Vẽ tia Cn là phân giác góc ngoài tại C. Cắt Ak tại N
c) Chứng minh góc Am vuông góc Ak, Cn vuông góc với Ck
d) Chứng minh góc AmC bằng góc CnA
e) Khi góc B= x độ . Tính số đo AkC qua x
a: \(\widehat{KAC}+\widehat{KCA}=\dfrac{180^0-72^0}{2}=54^0\)
nên \(\widehat{AKC}=126^0\)
c: Vì Am và AK là hai tia phân giác của hai góc kề bù
nên Am⊥AK
Vì Cn và CK là hai tia phân giác của hai góc kề bù
nên Cn⊥CK
e: \(\widehat{KAC}+\widehat{KCA}=\dfrac{180^0-x}{2}\)
\(\Leftrightarrow\widehat{AKC}=\dfrac{360^0-180^0+x}{2}=\dfrac{180^0+x}{2}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A bằng 70 độ , tia phân giác góc B và góc C cắt nhau tại I , các tia phân giác góc ngoài tại đỉnh B và C cát nhau tại K. Tính các góc của tứ giác BICK
Ta có:
ICK=ICB+KCB
=1/2ACB+1/2BCx
=1/2 180=90
Hoàn toàn tương tự thì:IBK=90
Xét tứ giác BICK có:
CIB+IBC+ICB+CKB=360
=>CIB=360-(IBC+ICB+CKB)=360-235=125
Vậy các góc của tứ giác BICK là CIB=125, CKB=55
IBK=ICK=90
hình bạn tự vẽ nha !chúc bạn học tốt
Cho tam giác ABC có B=72 độ, các tia phân giác của A và C cắt nhau ở K . Tính góc AKC
Cho tam giác ABC. Các tia phân giác của các góc B và C cát nhau tại I. chứng minh rằng AI là tia phân giác của góc A.
Hướng dẫn: từ I, kẻ các đường vuông góc với các cạnh của tam giác ABC.
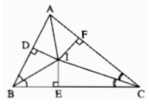
Kẻ: ID⊥AB, IE⊥BC, IF⊥AC
Xét hai tam giác vuông ΔIBD và ΔIEB, ta có:
∠(DBI) =∠(EBI) (gt)
∠(IDB) =∠(IEB) =90o
BI cạnh chung
Suy ra: ΔIDB= ΔIEB(cạnh huyền, góc nhọn)
Suy ra: ID = IE ( hai cạnh tương ứng)
Xét hai tam giác vuông ΔIEC và ΔIFC, ta có:
∠(ECI) =∠(FCI)
∠(IEC) =∠(IFC) =90o
CI cạnh huyền chung
Suy ra: ΔIEC= ΔIFC(cạnh huyền góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông ΔIDA và ΔIFA, ta có:
ID=IF
∠(IDA) =∠(IFA) =90o
AI cạnh huyền chung
Suy ra: ΔIDA= ΔIFA(cạnh huyền.cạnh góc vuông)
Suy ra: ∠(DAI) =∠(FAI) (hai góc tương ứng)
Vậy AI là tia phân giác góc A
Đúng 0
Bình luận (0)
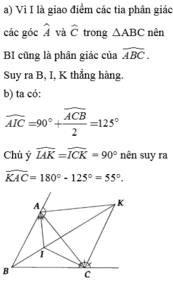
Cho tam giác ABC. Các đường phân, giác các góc ngoài tại đỉnh A và C cắt nhau ở K.a) Cho các tia phân giác các góc A và C trong tam giác ABC cắt nhau ở I Chứng minh B, I, K thẳng hàng.b) Cho biết
A
B
C
^
70
°
. Tính
A
K
C
^
?
Đọc tiếp
Cho tam giác ABC. Các đường phân, giác các góc ngoài tại đỉnh A và C cắt nhau ở K.
a) Cho các tia phân giác các góc A và C trong tam giác ABC cắt nhau ở I Chứng minh B, I, K thẳng hàng.
b) Cho biết A B C ^ = 70 ° . Tính A K C ^ ?