Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy là a, b (a < b) và độ dài đường sinh là l (a, b, l có cùng đơn vị đo).

Những câu hỏi liên quan
Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy là a, b (a < b) và độ dài đường sinh là l (a, b, l có cùng đơn vị đo).
Áp dụng công thức tính diện tích xung quanh hình nón cụt ta có:
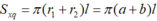
Đúng 0
Bình luận (0)
Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy là a, b (a < b) và độ dài đường sinh là l (a, b, l có cùng đơn vị đo).
Giải:
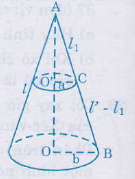
Kí hiệu như hình vẽ. Ta có hai tam giác vuông AO'C và AOB đồng dạng vì có góc chung.
Nên =>
=> =>
Diện tích xung quanh của hình nón lớn:
Sxq nón lớn = π.r.l =π.b.l
Diện tích xung quanh của hình nón nhỏ:
Sxq nón nhỏ = π.r.l1= π.a. = π.
Diện tích xung quanh của hình nón cụt:
Sxq nón cụt = Sxq nón lớn -Sxq nón nhỏ
=
=
Đúng 0
Bình luận (0)
Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy là a,b (a<b) và độ dài đường sinh là l ( a,b,l có cùng đơn vị) sgk tr 119 tập 2
Cho hình nón cụt như hình vẽ Biết rằng bán kính của đáy nhỏ là r = 3cm, bán kính của đáy lớn là R = 6cm, độ dài AC = 4cm. Hãy tính diện tích xung quanh, diện tích toàn phần, và thể tích của hình nón cụt

Lời giải:
Diện tích xung quanh hình nón:
$\pi (r+R).l=\pi (6+3).4=36\pi$ (cm vuông)
Diện tích toàn phần:
$36\pi+\pi r^2+\pi R^2=36\pi +\pi.3^2+\pi. 6^2=81\pi$ (cm vuông)
Thể tích:
Chiều cao hình nón: $\sqrt{4^2-(6-3)^2}=\sqrt{7}$ (cm)
$\frac{1}{3}\pi (r^2+R^2+r.R)h=\frac{1}{3}\pi (3^2+6^2+3.6).\sqrt{7}=21\sqrt{7}\pi$ (cm khối)
Đúng 0
Bình luận (0)
Bài 3: Cho hình nón cụt như hình vẽ Biết rằng bán kính của đáy nhỏ là r= 3cm, bán kính của đáy lớn là R = 6cm, độ dài AB = 4cm. Hãy tính diện tích xung quanh, diện tích toàn phần, và thể tích của hình nón cụt
Bài 3: Cho hình nón cụt như hình vẽ Biết rằng bán kính của đáy nhỏ là r= 3cm, bán kính của đáy lớn là R = 6cm, độ dài AB = 4cm. Hãy tính diện tích xung quanh, diện tích toàn phần, và thể tích của hình nón cụt
Hình vẽ đâu bn.(không có hình thì mik ko bt AB là đường sinh hay chiều cao nhé. Nhưng thường thì AB là đường sinh)
(nếu đề bài AB là đường cao thì bn đăng lại nhé)
\(Sxq=\pi\left(r+R\right)l=\pi\left(3+6\right)4=36\pi\left(cm^2\right)\)
\(Stp=\pi\left(r+R\right)l+\pi\left(r^2+R^2\right)=36\pi+\pi\left(3^2+6^2\right)=36\pi+45\pi\)
\(=81\pi\left(cm^2\right)\)
có: \(h=\sqrt{l^2-\left(R-r\right)^2}=\sqrt{4^2-\left(6-3\right)^2}=\sqrt{7}cm\)
\(V=\dfrac{1}{3}\pi\left(r^2+R^2+rR\right).h\)\(=\dfrac{1}{3}\pi.\left(3^2+6^2+3.6\right).\sqrt{7}=21\sqrt{7}.\pi\left(cm^3\right)\)
Đúng 0
Bình luận (0)
Cho hình nón có bán kính đáy là
r
3
và độ dài đường sinh l4. Tính diện tích xung quanh S của hình nón đã cho.
Đọc tiếp
Cho hình nón có bán kính đáy là r = 3 và độ dài đường sinh l=4. Tính diện tích xung quanh S của hình nón đã cho.
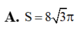
![]()
![]()
![]()
Cho hình nón có bán kính đáy là
r
2
và độ dài đường sinh l 4. Tính diện tích xung quanh S của hình nón đã cho A.
S
16
π
B.
S
8
2
π
C.
S
16
2
π
D.
S
4
2
π
Đọc tiếp
Cho hình nón có bán kính đáy là r = 2 và độ dài đường sinh l = 4. Tính diện tích xung quanh S của hình nón đã cho
A. S = 16 π
B. S = 8 2 π
C. S = 16 2 π
D. S = 4 2 π
Đáp án D
Diện tích xung quanh S = π r l = 4 2 π .
Đúng 0
Bình luận (0)
Cho hình nón có diện tích xung quanh bằng
2
π
a
2
,
bán kính đáy bằng a. Tính độ dài đường sinh l của hình nón đã cho. A.
l
a
2
. B.
l
2
a
. C.
l
a
D.
l
2
a
Đọc tiếp
Cho hình nón có diện tích xung quanh bằng 2 π a 2 , bán kính đáy bằng a. Tính độ dài đường sinh l của hình nón đã cho.
A. l = a 2 .
B. l = 2 a .
C. l = a
D. l = 2 a
Đáp án B
S x q = π R l = π a l = 2 π a 2 ⇒ l = 2 a .
Đúng 0
Bình luận (0)










