Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AC= a 2 mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60 o Tính theo a thể tích V của khối chóp S. ABC.
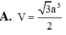
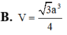
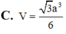
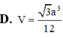
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AC=a 2 , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60 0 . Tính theo a thể tích V của khối chóp S.ABC
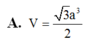
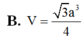
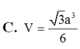
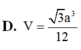
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, A C = a 2 , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60 0 . Tính theo a thể tích V của khối chóp S.ABC
A. V = 3 a 3 2
B. V = 3 a 3 4
C. V = 3 a 3 6
D. V = 3 a 3 12
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B , A C = a 2 , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên S A B , S B C tạo với mặt đáy các góc bằng nhau và bằng 60 ° . Tính theo a thể tích V của khối chóp S.ABC
A. V = 3 a 3 2
B. V = 3 a 3 4 V = 3 a 3 12
C. V = 3 a 3 6
D. V = 3 a 3 12
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AC = a 2 , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60 ° .Tính theo a thể tích V của khối chóp S. ABC.
A. V = 3 a 3 2
B. V = 3 a 3 4
C. V = 3 a 3 6
D. V = 3 a 3 12
Đáp án D
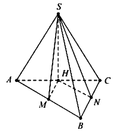
Gọi H là hình chiếu của S trên A C ⇒ S H ⊥ A B C
Kẻ H M ⊥ A B M ∈ A B , H N ⊥ A C N ∈ A C
Suy ra S A B ; A B C ^ = S B C ; A B C ^ = S M H ^ = S N H ^ = 60 °
⇒ ∆ S H M = ∆ S H N ⇒ H M = H N ⇒ H là trung điểm của AC
Tam giác SHM vuông tại H, có tan S M H ^ = S H H M ⇒ S H = a 3 2
Diện tích tam giác ABC là S ∆ A B C = 1 2 . A B . B C = a 2 2
Vậy thể tích cần tính là V = 1 3 . S H . S A B C = 1 3 . a 3 2 . a 2 2 = a 3 3 12
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A với AC = a 2 ; BC = a . Hai mặt phẳng (SAB) và (SAC) cùng tạo với mặt đáy (ABC) góc 60 0 . Tính khoảng cách từ điểm B đến mặt phẳng (SAC), biết rằng mặt phẳng (SBC) vuông góc với đáy (ABC).
A. 3 a 3 + 1
B. 3 a 4
C. 3 a 2 3 + 1
D. 3 a 2
Cho hình chóp S.ABC . có đáy ABC là tam giác vuông tại B . Các mặt bên (SAC); (SAB) cùng vuông góc với đáy, A C = 13 2 B C = 3 , SC = 2. Gọi α là góc hợp bởi hai mặt phẳng (ABC), (SBC) . Giá trị biểu thức T = 2 sin α 2 + 2 3 3 cos α 2
A. 0
B. 1
C. 2
D. 3
Đáp án C
Ta dễ suy ra
![]()
Ta có
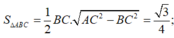
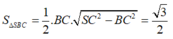
Lại có
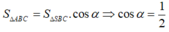
![]()
Chọn C .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, với ; AC=\(\frac{a}{2}\) BC a . Hai mặt phẳng (SAB) và (SAC) cùng tạo với mặt đáy (ABC) góc 600 . Tính thể tích khối chóp S.ABC và khoảng cách từ B tới mặt phẳng (SAC) theo a biết mặt phẳng (SBC) vuông góc với đáy (ABC).
Kẻ SH vuông góc với BC tại H => SH vuông góc với (ABC)
Kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N
Ta có góc SMH = góc SNH = 60 độ
Dễ thấy tam giác SHM = tam giác SHN => HM = HN
Ta có HM = HB.sin 30 = 1/2 HB hay HB = 2 HM
HN = HC.sin 60 = HC.căn 3 /2 => HC = 2/căn 3.HN = 2/căn 3 .HM
=> BC = a = HB + HC = ( 2 + 2/căn 3).HM
=> HM = a/(2 + 2/căn 3) = a.căn 3 /(2+ 2.căn 3)
=> SH = HM.tan 60 = 3a/(2+2.căn 3)
Có AB = BC/2 = a/2
AC = BC.căn 3/2 = a.căn 3/2
S(ABC) = 1/2.AB.AC = 1/8.a^2.căn 3
=> V(SABC) = 1/3.3a/(2+2.căn 3) . 1/8.a^2.căn 3 = a^3.căn 3 /[16.(1+ căn 3)]
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a Các mặt bên (SAB),(SAC),(SBC) lần lượt tạo với đáy các góc lần lượt 30 độ, 45 độ, 60 độ Tính thể tích V của khối chóp S.ABC biết rằng hình chiếu vuông góc của S trên mặt phẳng (ABC) nằm bên trong tam giác ABC.
A. V = a 3 3 4 + 3
B. V = a 3 3 2 4 + 3
C. V = a 3 3 4 4 + 3
D. V = a 3 3 8 4 + 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB=AC=a, biết tam giác cân SAB cân tại S và nằm trong mặt phẳng vuông góc với (ABC). Mặt phẳng (SAC) hợp với mặt phẳng (ABC) một góc bằng . Thể tích của khối chóp S.ABC bằng
A. a 3 3
B. a 3 4
C. a 3 9
D. a 3 12