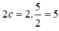Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là:
A. x 2 25 + y 2 16 = 1.
B. x 2 5 + y 2 4 = 1.
C. x 2 25 + y 2 9 = 1.
D. x 5 + y 4 = 1.
Những câu hỏi liên quan
Cho elip (E) có phương trình:
x
2
100
+
y
2
36
1
a, Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip (E) và vẽ elip đó.b, Qua tiêu điểm của elip dựng đường song song với Oy và cắt elip tại hai điểm M và N. Tính độ dài đoạn MN.
Đọc tiếp
Cho elip (E) có phương trình: x 2 100 + y 2 36 = 1
a, Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip (E) và vẽ elip đó.
b, Qua tiêu điểm của elip dựng đường song song với Oy và cắt elip tại hai điểm M và N. Tính độ dài đoạn MN.
a) (E):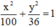 
có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
+ Tọa độ các đỉnh của elip là: A1(-10; 0); A2(10; 0); B1(0; -6); B2(0; 6)
+ Tọa độ hai tiêu điểm của elip: F1(-8; 0) và F2(8; 0)
+ Vẽ elip:
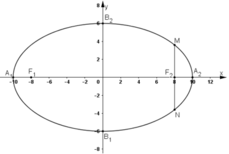
b) Ta có: M ∈ (E) ⇒ MF1 + MF2 = 2a = 20 (1)
MN // Oy ⇒ MN ⊥ F1F2 ⇒ MF12 – MF22 = F1F22 = (2c)2 = 162
⇒ (MF1 + MF2).(MF1 – MF2) = 162
⇒ MF1 – MF2 = 12,8 (Vì MF1 + MF2 = 20) (2).
Từ (1) và (2) ta có hệ phương trình
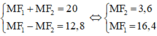
Vậy MN = 2.MF2 = 7,2.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm
F
1
,
F
2
dưới một góc bằng
120
°
. Phương trình chính tắc của elip đã cho là
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm F 1 , F 2 dưới một góc bằng 120 ° . Phương trình chính tắc của elip đã cho là
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm
F
1
,
F
2
dưới một góc bằng
120
∘
. Phương trình chính tắc của elip đã cho là A.
x
2
8
+
y
2
4
1
B.
x...
Đọc tiếp
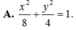
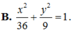
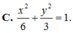
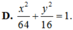
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm F 1 , F 2 dưới một góc bằng 120 ∘ . Phương trình chính tắc của elip đã cho là
A. x 2 8 + y 2 4 = 1
B. x 2 36 + y 2 9 = 1
C. x 2 6 + y 2 3 = 1
D. x 2 64 + y 2 16 = 1
cho elip (e) có pt chính tắc: x^2/9 + y^2/4=1
a) tìm tọa độ đỉnh, tiêu điểm f1, f2, và tâm sai của (e)
b) tìm tọa độ điểm m thuộc (e) thõa mãn mf1 -mf2=2
(f1 là tiêu điểm bên trái của elip)
Cho elip (E) có các tiêu điểm
F
1
-
5
;
0
,
F
2
5
;
0
và một điểm M nằm trên (E) sao cho chu vi của tam giác
M
F
1
F
2
bằng 30. Khi đó phương trình chính tắc của elip là: A. ...
Đọc tiếp
Cho elip (E) có các tiêu điểm F 1 - 5 ; 0 , F 2 5 ; 0 và một điểm M nằm trên (E) sao cho chu vi của tam giác M F 1 F 2 bằng 30. Khi đó phương trình chính tắc của elip là:
A. x 2 75 + y 2 100 = 1
B. 100 x 2 + 75 y 2 = 1
C. 75 x 2 + 100 y 2 = 1
D. x 2 100 + y 2 75 = 1
Cho elip (E): x 2 16 + y 2 9 = 1 . Tìm tọa độ các đỉnh, các tiêu điểm và vẽ elip đó.
Elip (E):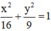 
có a = 4, b = 3 ⇒ c2 = a2 – b2 = 7 ⇒ c = √7.
+ Các đỉnh của elip là: A1(–4; 0); A2(4; 0); B1(0; –3); B2(0; 3).
+ Tiêu điểm của elip: F1(–√7; 0); F2(√7; 0).
+ Vẽ elip:
Đúng 0
Bình luận (0)
Cho elip có phương trình:
x
2
9
+
y
2
4
1
Khi đó tọa độ hai đỉnh trên trục nhỏ của elip là. A. B1( -2; 0) và B2( 2;0) B. B1( 3;0) và B2( 2; 0) C. B1( -3;0) và B2( -2;0) D. B1( 3;0) và B2(-3;0)
Đọc tiếp
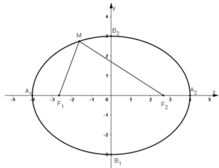
Cho elip có phương trình: x 2 9 + y 2 4 = 1 Khi đó tọa độ hai đỉnh trên trục nhỏ của elip là.
A. B1( -2; 0) và B2( 2;0)
B. B1( 3;0) và B2( 2; 0)
C. B1( -3;0) và B2( -2;0)
D. B1( 3;0) và B2(-3;0)
Ta có: b2= 4 mà b> 0 nên b= 2
- Hai đỉnh trên trục nhỏ là: B1( -2; 0) và B2( 2;0)
Chọn A
Đúng 0
Bình luận (0)
Cho elip có phương trình:
x
2
4
+
y
2
1
1
Khi đó tọa độ hai đỉnh trên trục lớn của elip là. A. A1( -1; 0) và A2( 1;0) B. A1( 0; -1) và A2( 0; 1) C. A1( 2;0) và A2( 1; 0) D. A1( (-2;0) và A2(2;0)
Đọc tiếp
Cho elip có phương trình: x 2 4 + y 2 1 = 1 Khi đó tọa độ hai đỉnh trên trục lớn của elip là.
A. A1( -1; 0) và A2( 1;0)
B. A1( 0; -1) và A2( 0; 1)
C. A1( 2;0) và A2( 1; 0)
D. A1( (-2;0) và A2(2;0)
Ta có: a2= 4 mà a> 0 nên a= 2
- Hai đỉnh trên trục lớn là: . A1( (-2;0) và A2(2;0)
Chọn D
Đúng 0
Bình luận (0)
Cho elip (E) đi qua điểm A(-3;0) và có tâm sai e = 5/6. Tiêu cự của (E) là:
A. 10
B. 5/3
C. 5
D. 10/3
Đáp án: C
Cho elip (E) đi qua điểm A(-3;0) và có tâm sai
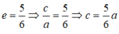
Giả sử elip có dạng:
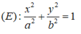
Vì (E) đi qua điểm
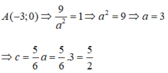
Vậy elip (E) có tiêu cự là: 
Đúng 0
Bình luận (0)