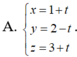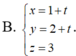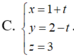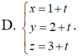Vị trí tương đối của đường thẳng 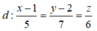 và mặt phẳng (P): x + y + z - 10 = 0 là:
và mặt phẳng (P): x + y + z - 10 = 0 là:
A. d ⊂ (P)
B. cắt nhau
C. song song
D. Đáp án khác
Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa đường thẳng a và cắt mặt phẳng (P) theo giao tuyến là đường thẳng b. Vị trí tương đối của hai đường thẳng a và b là:
A. chéo nhau
B. cắt nhau
C. song song
D. trùng nhau
Cho a,b là hai đường thẳng song song và cách nhau một khoảng 3cm.Lấy điểm I trên a và vẽ đường tròn (I;3;5cm).Khi đó vị trí tương đối của đường thẳng b với đường tròn ( I);
A cắt nhau B không cắt nhau C tiếp xúc D đáp án khác
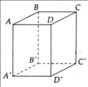
Cho hình hộp chữ nhật ABCD.A'B'C'D' như hình vẽ trên.
a) Nêu vị trí tương đối của các cặp đường thẳng AB' và C'D; B'D' và AD; AC và A'C.
b) BC’ song song với (ADD'A') không? Vì sao? Chứng minh (BCC'B') song song với (ADD'A').
c) AC' và CA'có cắt nhau không? Vì sao?
d) Hai mặt phẳng (ACC'A') và (BDD'B') có cắt nhau không? Nếu cắt thì cắt theo đường thẳng chung nào?
Tương tự 1A
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')
Vị trí tương đối của đường thẳng d: x = 2 + 4t, y = 3 + t, z = -5t và mặt phẳng (P): x + y + z - 3 = 0 là:
A. d ⊂ (P)
B. cắt nhau
C. song song
D. Đáp án khác
Đáp án C
Đường thẳng d đi qua điểm M(2 ;3 ;0) và có vectơ chỉ phương là u d → = (4; 1; -5), mặt phẳng (P) có vectơ pháp tuyến là u p → = (1; 1; 1). Ta có:
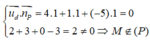
Suy ra đường thẳng d song song với mặt phẳng (P).
Vị trí tương đối của đường thẳng d: x = 1 + 2t, y = 1 - t, z = 1 - t và mặt phẳng (P): x + y + z - 3 = 0 là:
A. d ⊂ (P)
B. cắt nhau
C. song song
D. Đáp án khác
Đáp án A
Đường thẳng d đi qua điểm A( 1 ; 1 ;1); có một vecto chỉ phương là ( 2; -1; -1)
Mặt phẳng (P) có vecto pháp tuyến là
Ta có: u → . n → = 2.1 + (-1).1 + (-1).1 = 0 và A ∈ (P)
Suy ra, đường thẳng d thuộc mặt phẳng (P).
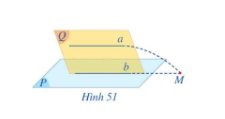
Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyển b. (Hình 51)
a) Giả sử a cắt b tại M. Đường thẳng a có cắt mặt phẳng (P) tại M hay không?
b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?
a) Ta có a ∩ b = {M} nên M ∈ b
Mà b ⊂ (P), do đó M ∈ (P).
Lại có M ∈ a.
Vậy đường thẳng a cắt mặt phẳng (P) tại M.
b) Theo câu a, nếu a cắt b tại M thì a cắt (P) tại M, điều này mâu thuẫn với giả thiết đường thẳng a song song với mặt phẳng (P).
Do đó a và b không cắt nhau và cùng nằm trong mặt phẳng (Q).
Suy ra a // b.
Vậy hai đường thẳng a và b song song với nhau.
Cho đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng \(\Delta \).
a) Qua một điểm O thuộc (P), kẻ đường thẳng a' song song với a. Nêu vị trí tương đối giữa a' và (P).
b) Nêu vị trí tương đối giữa a và (P).
a: \(\text{Δ}\perp a\)
a//a'
=>Δ vuông góc a'
mà Δ vuông góc (P)
nên a'//(P) hoặc \(a'\subset\left(P\right)\)
mà \(a'\cap\left(P\right)=\left\{O\right\}\)
nên a' nằm trong (P)
b: a'//a
\(a'\subset\left(P\right)\)
=>a//(P) hoặc \(a\subset\left(P\right)\)
Cho hình hộp chữ nhật ABCD.A'B'C'D' như hình vẽ. Cắt
D
hình hộp theo mặt cắt MNPQ với M là trung điểm của AB và
(MNPQ) song song (AA'D'D).
a) Chứng minh NQ // (BCC'B').
b) Nếu vị trí tương đối của các cặp đường thẳng AN và BD; PB' và MN.
c) Cho AA' = 50 cm và ND' = DM = 50/2 cm. Khi đó AMND.A'QPD' là hình gì?
Viết phương trình đường thẳng d qua A(1;2;3) cắt đường thẳng d 1 : x 2 = y 1 = z - 2 1 và song song với mặt phẳng (P): x+y-z-2=0