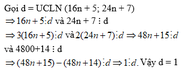Gọi d = (2n+5;3n+7) (d thuộc N) 
=> (2n+5) chia hết cho d và (3n +7) chia hết cho d 
=> 3.(2n + 5) - 2.(3n + 7) chia hết cho d 
=> 1 chia hết cho d 
=> d = 1 (vì d thuộc N) 
=> ƯCLN(2n + 5 ; 3n + 7) = 1 
=> Phân số 2n+5/3n+7 tối giản với mọi n thuộc N

ko chắc, bn tham khảo

Học tốt

goi d la uoc nguyen to cua 2n+5 va 3n+7

Suy ra 2n+5 va 3n+7 chia het cho d

Suy ra 3(2n+5) va 2(3n+7) chia het cho d

Suy ra 6n+15 va 6n+14 chia het cho d

Suy ra 6n+15-6n+14 chia het cho d

Suy ra 1 chia het cho d

Suy ra d thuoc Ư(1)=1

Suy ra 2n+5/3n+7 la phan so toi gian

Gọi d = ƯCLN ( 2n + 5 ; 3n + 7 )

Ta có :

2n + 5 \(⋮\)d ; 3n + 7 \(⋮\)d

=> 3 ( 2n + 5 ) \(⋮\)d ; 2 ( 3n+ 7 ) \(⋮\)d

=> 6n + 15 \(⋮\); 6n + 14 \(⋮\)d

=> ( 6n + 15 ) - ( 6n + 14 ) \(⋮\)d

=> 1 \(⋮\)d

=> d = { 1 ; - 1 }

=> \(\frac{2n+5}{3n+7}\)là phân số tối giản

Đặt ƯCLN\(\left(16n+5;24n+7\right)=d\)

=> 16n + 5 chia hết cho d và 24n + 7 chia hết cho d.

=> 3.(16n + 5) - 2.(24n + 7) chia hết cho d.

=> 48n + 15 - 38n + 14 chia hết cho d

=> 1 chia hết cho d

=> d = 1

  suy ra điều phải chứng tỏ
 

Gọi d là UCLN(16n+5;24n+7)

=>16n+5 chia hết cho d và 24n+7 chia hết cho d

Vì:16n+5 chia hết cho d=>48n+15 chia hết cho d

     24n+7 chia hết cho d=>48n+14 chia hết cho d

Ta có:(48n+15)-(48n+14) chia hết cho d

         =          1 chia hết cho d

Vì d=1 nên \(\frac{18n+5}{24n+7}\)là phân số tối giản với mọi n.

Mình làm bài này rồi,đề thi HSG lớp 6 có bài này.

Dễ quá thôi!

Đặt d = ƯCLN( 14n + 3, 21n + 5 ) ( d ∈ N* )

Ta có: 14n + 3 ⋮ d và 21n + 5 ⋮ d

⇒ 3( 14n + 3 ) ⋮ d và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d

⇒ ( 42n + 9 ) – ( 42n + 10 ) ⋮ d ⇒ 1 ⋮ d . Do đó d = 1  

Vậy 14 n + 3 21 n + 5  là phân số tối giản

Đặt d = ƯCLN( 14n + 3, 21n + 5 ) ( d ∈ N* )

Ta có: 14n + 3 ⋮ d và 21n + 5 ⋮ d

⇒ 3( 14n + 3 ) ⋮ d và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d

⇒ ( 42n + 9 ) – ( 42n + 10 ) ⋮ d ⇒ 1 ⋮ d . Do đó d = 1

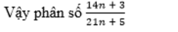  là phân số tối giản.

Đặt \(\left(14n+3,21n+5\right)=d\).

Suy ra 

\(\hept{\begin{cases}14n+3⋮d\\21n+5⋮d\end{cases}}\Rightarrow2\left(21n+5\right)-3\left(14n+3\right)=1⋮d\Rightarrow d=1\).

Do đó ta có đpcm. 

Khó dữ zậy

Có : \(\frac{n+5}{n+6}=\frac{n+6-1}{n+6}=\frac{n+6}{n+6}-\frac{1}{n+6}=1-\frac{1}{n+6}\)

Để \(\frac{n+5}{n+6}\in Z\Rightarrow n+6\inƯ\left(1\right)\)

\(Ư\left(1\right)\in\left\{\pm1\right\}\Rightarrow n+6\in\left\{1;-1\right\}\)

\(\Rightarrow n\in\left\{-5;-7\right\}\)

\(\Leftrightarrow\left\{{}\begin{matrix}2n+6⋮a\\2n+5⋮a\end{matrix}\right.\Leftrightarrow a=1\)

Vậy: 2n+5/n+3 là một phân số tối giản

gọi d là ước chung của n+3 và 2n+5 với d∈N

⇒n+3⋮d và 2n+5⋮d

⇒(n+3)-(2n+5)⋮d ⇒2(n+3)-(2n+5)⋮d⇔1⋮d⇒d=1∈N

⇒ƯC(n+3 và 2n+5)=1

⇒ƯCLN(n+3 và 2n+5)=1⇒\(\dfrac{2n+5}{n+3}\),(n∈N) là phân số tối giản