Đường thẳng nào dưới đây là 1 đường chuẩn của Elip x 2 16 + y 2 12 = 1
A. x + 4 3 = 0
B. x+ 2= 0
C. x - 3 4 = 0
D. x+ 8= 0
Cho biết mỗi đường conic có phương trình dưới đây là đường conic dạng nào ( elip, hypebol, parabol) và tìm tọa độ tiêu điểm của đường conic đó.
a) \({y^2} = 18x\)
b) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\)
c) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\)
a) Đây là một parabol. Tiêu điểm của parabol có tọa độ là: \(F\left({\frac{9}{2};0} \right)\).
b) Đây là một elip. Tiêu điểm của elip có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} - {b^2}} ;0} \right) = \left( { - \sqrt {39} ;0} \right)\\{F_2}\left( {\sqrt {{a^2} - {b^2}} ;0} \right) = \left( {\sqrt {39} ;0} \right)\end{array} \right.\)
c) Đây là một hyperbol. Tiêu điểm của hypebol có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} + {b^2}} ;0} \right) = \left( { - 5;0} \right)\\{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right) = \left( {5;0} \right)\end{array} \right.\)
Đường thẳng nào dưới đây là đường chuẩn của Hyperbol x 2 16 - y 2 12 = 1
A. x - 3 4 = 0
B. x+2=0
C. x-4=0
D. x + 8 7 7 = 0
Đáp án : B
Ta có a 2 = 16 b 2 = 12 c 2 = a 2 + b 2 ⇒ a = 4 b = 2 3 c = 2
Tâm sai e = c a = 2 . Đường chuẩn: x+ 2= 0 và x-2 =0 .
Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi 2 đường thẳng ∆ 1: x+ 2y -3= 0 và ∆2: 2x – y + 3= 0.
A. x+ 3y-2= 0 và x= 3y.
B. 3x= - y và x-3y-6= 0.
C. 3x+ y= 0 và –x+ 3y- 6= 0.
D.Đáp án khác
Gọi M(x; y) là điểm thuộc đường phân giác tạo bởi 2 đường thẳng đã cho.
![]()
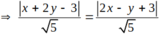
![]()
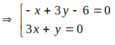
Chọn C.
Đường thẳng nào dưới đây là TCN của C: y = 1 + 2 x 1 - x

![]()
![]()
![]()
Hỏi đường thẳng giao tuyến của hai mặt phẳng (P): x+2y-z+1=0 và (Q): x+y+2z+3=0 là đường thẳng nào dưới đây ?
A. x + 5 - 5 = y + 2 3 = z 1
B. x + 5 - 5 = y - 2 3 = z - 1 1
C. x + 5 5 = y + 2 - 3 = z - 1
D. x + 5 5 = y - 2 - 3 = z - 1
Phương trình nào sau đây là phương trình chính tắc của đường elip?
A. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{9} = 1\)
B. \(\frac{{{x^2}}}{1} + \frac{{{y^2}}}{6} = 1\)
C. \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{1} = 1\)
D. \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} = 1\)
Trong không gian Oxyz, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng d : x - 1 2 = y - 2 - 1 = z 3
![]()
![]()
![]()
![]()
Đường thẳng ∆ nào dưới đây là đường vuông góc chung của d1, d2 với: d 1 : x 4 = y - 1 - 4 = z + 1 - 1 ; d 2 : x + 1 2 = y - 1 1 = z - 3 - 1
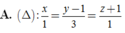
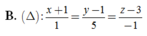
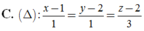
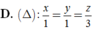
trong mặt phẳng oxy vecto nào dưới đây là một vecto pháp tuyến của đường thẳng d {x=-2-t;y=-1+2t