Phân tích vế trái thành nhân tử, giải phương trình sau: x2 – x – (3x – 3) = 0

Những câu hỏi liên quan
Phân tích vế trái thành nhân tử, giải phương trình sau: (x2 – 4) + (x – 2)(3 – 2x) = 0
(x2 – 4) + (x – 2)(3 – 2x) = 0
⇔ (x – 2)(x + 2) + (x – 2)(3 – 2x) = 0
⇔ (x – 2)[(x + 2) + (3 – 2x)] = 0
⇔ (x – 2)(5 – x) = 0
⇔ x – 2 = 0 hoặc 5 – x = 0
+ x – 2 = 0 ⇔ x = 2
+ 5 – x = 0 ⇔ x = 5.
Vậy tập nghiệm của phương trình là S = {2; 5}.
Đúng 0
Bình luận (0)
Phân tích vế trái thành nhân tử, giải phương trình sau: x3 – 3x2 + 3x – 1 = 0
x3 – 3x2 + 3x - 1 = 0
⇔ (x – 1)3 = 0 (Hằng đẳng thức)
⇔ x – 1 = 0
⇔ x = 1.
Vậy tập nghiệm của phương trình là S={1}.
Đúng 0
Bình luận (0)
phân tích vế trái thành nhân tử, giải phương trình sau: 2x(x – 3) + 5(x – 3) = 0
2x(x – 3) + 5(x – 3) = 0
⇔ (2x + 5)(x – 3) = 0
⇔ 2x + 5 = 0 hoặc x – 3 = 0
+ 2x + 5 = 0 ⇔2x = -5 ⇔ x = -5/2
+ x – 3 = 0 ⇔x = 3.
Vậy phương trình có tập nghiệm 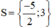
Đúng 0
Bình luận (0)
Phân tích vế trái thành nhân tử, giải phương trình sau: x(2x – 7) – 4x + 14 = 0
x(2x – 7) – 4x + 14 = 0
⇔ x.(2x - 7) – (4x – 14) = 0
⇔ x(2x – 7) – 2(2x – 7) = 0
⇔(x – 2)(2x – 7) = 0
⇔ x – 2 = 0 hoặc 2x – 7 = 0
+ x – 2 = 0 ⇔ x = 2.
+ 2x – 7 = 0 ⇔ 2x = 7 ⇔ x = 7/2
Vậy tập nghiệm của phương trình là 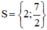
Đúng 0
Bình luận (0)
Phân tích vế trái thành nhân tử, giải phương trình sau: (2x – 5)2 – (x + 2)2 = 0
(2x – 5)2 – (x + 2)2 = 0
⇔ [(2x – 5) + (x + 2)].[(2x – 5) – (x + 2)]= 0
⇔ (2x – 5 + x + 2).(2x – 5 – x - 2) = 0
⇔ (3x – 3)(x – 7) = 0
⇔ 3x – 3 = 0 hoặc x – 7 = 0
+ 3x – 3 = 0 ⇔3x = 3 ⇔ x = 1.
+ x – 7 = 0 ⇔ x = 7.
Vậy phương trình có tập nghiệm S = {1; 7}.
Đúng 0
Bình luận (0)
Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:
a) x3 – 3x2 + 3x – 1 = 0;
b) x(2x - 7) - 4x + 14 = 0
a) x3 – 3x2 + 3x – 1 = 0 ⇔ (x – 1)3 = 0 ⇔ x = 1.
Vậy tập nghiệm của phương trình là x = 1
b) x(2x - 7) - 4x + 14 = 0 ⇔ x(2x - 7) - 2(2x - 7) = 0
⇔ (x - 2)(2x - 7) = 0 ⇔ x - 2 = 0 hoặc 2x - 7 = 0
1) x - 2 = 0 ⇔ x = 2
2) 2x - 7 = 0 ⇔ 2x = 7 ⇔ x = \(\frac{7}{2}\)
Vậy tập nghiệm của phương trình là S = {2;\(\frac{7}{2}\)}
Đúng 0
Bình luận (0)
a) x3 – 3x2 + 3x – 1 = 0
⇔ (x – 1)3 = 0
⇔ x = 1.
Vậy tập nghiệm của phương trình là x = 1
b) x(2x - 7) - 4x + 14 = 0
⇔ x(2x - 7) - 2(2x - 7) = 0
⇔ (x - 2)(2x - 7) = 0 ⇔ x - 2 = 0 hoặc 2x - 7 = 0
1) x - 2 = 0 ⇔ x = 2
2) 2x - 7 = 0 ⇔ 2x = 7 ⇔ x = 2 7
Vậy tập nghiệm của phương trình là S = {2; 2 7 }
Đúng 0
Bình luận (0)
Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:
a) (2x – 5)2 – (x + 2)2 = 0;
b) x2 – x – (3x - 3) = 0
a) (2x – 5)2 – (x + 2)2 = 0 ⇔ (2x - 5 - x - 2)(2x - 5 + x + 2) = 0
⇔ (x - 7)(3x - 3) = 0 ⇔ x - 7 = 0 hoặc 3x - 3 = 0
1) x - 7 = 0 ⇔ x = 7
2) 3x - 3 = 0 ⇔ 3x = 3 ⇔ x = 1
Vậy tập nghiệm phương trình là: S= { 7; 1}
b) x2 – x – (3x - 3) = 0 ⇔ x2 – x – 3x + 3 = 0
⇔ x(x - 1) - 3(x - 1) = 0 ⇔ (x - 3)(x - 1) = 0
⇔ x = 3 hoặc x = 1
Vậy tập nghiệm của phương trình là S = {1;3}
Đúng 0
Bình luận (0)
a) (2x – 5)2 – (x + 2)2 = 0 ⇔ (2x - 5 - x - 2)(2x - 5 + x + 2) = 0 ⇔ (x - 7)(3x - 3) = 0 ⇔ x - 7 = 0 hoặc 3x - 3 = 0 1) x - 7 = 0 ⇔ x = 7 2) 3x - 3 = 0 ⇔ 3x = 3 ⇔ x = 1 Vậy tập nghiệm phương trình là: S= { 7; 1} b) x2 – x – (3x - 3) = 0 ⇔ x2 – x – 3x + 3 = 0 ⇔ x(x - 1) - 3(x - 1) = 0 ⇔ (x - 3)(x - 1) = 0 ⇔ x = 3 hoặc x = 1 Vậy tập nghiệm của phương trình là S = {1;3}
Đúng 0
Bình luận (0)
a) (2x – 5)2 – (x + 2)2 = 0 ⇔ (2x - 5 - x - 2)(2x - 5 + x + 2) = 0 ⇔ (x - 7)(3x - 3) = 0 ⇔ x - 7 = 0 hoặc 3x - 3 = 0 1) x - 7 = 0 ⇔ x = 7 2) 3x - 3 = 0 ⇔ 3x = 3 ⇔ x = 1 Vậy tập nghiệm phương trình là: S= { 7; 1} b) x2 – x – (3x - 3) = 0 ⇔ x2 – x – 3x + 3 = 0 ⇔ x(x - 1) - 3(x - 1) = 0 ⇔ (x - 3)(x - 1) = 0 ⇔ x = 3 hoặc x = 1 Vậy tập nghiệm của phương trình là S = {1;3}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bằng cách phân tích vế trái thành nhân tử, giải các PT sau:
a) \(2x.\left(x-3\right)+5\left(x-3\right)\)
b) \(\left(x^2-4\right)+\left(x-2\right).\left(3-2x\right)=0\)
c) \(x^3-3x^2+3x-1=0\)
a: =(x-3)(2x+5)
b: \(\Leftrightarrow\left(x-2\right)\left(x+2+3-2x\right)=0\)
=>(x-2)(5-x)=0
=>x=2 hoặc x=5
c: =>x-1=0
hay x=1
Đúng 1
Bình luận (0)
Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:
a) 2x(x - 3) + 5(x - 3) = 0
b) (x2 - 4) + (x - 2)(3 - 2x) = 0
a) 2x(x - 3) + 5(x - 3) = 0 ⇔ (x - 3)(2x + 5) = 0 ⇔ x - 3 = 0 hoặc 2x + 5 = 0
1) x - 3 = 0 ⇔ x = 3
2) 2x + 5 = 0 ⇔ 2x = -5 ⇔ x = -2,5
Vậy tập nghiệm của phương trình là S = {3;-2,5}
b) (x2 - 4) + (x - 2)(3 - 2x) = 0 ⇔ (x - 2)(x + 2) + (x - 2)(3 - 2x) = 0
⇔ (x - 2)(x + 2 + 3 - 2x) = 0 ⇔ (x - 2)(-x + 5) = 0 ⇔ x - 2 = 0 hoặc -x + 5 = 0
1) x - 2 = 0 ⇔ x = 2
2) -x + 5 = 0 ⇔ x = 5
Vậy tập nghiệm của phương trình là S = {2;5}
Đúng 0
Bình luận (0)
a) 2x(x - 3) + 5(x - 3) = 0 ⇔ (x - 3)(2x + 5) = 0 ⇔ x - 3 = 0 hoặc 2x + 5 = 0 1) x - 3 = 0 ⇔ x = 3 2) 2x + 5 = 0 ⇔ 2x = -5 ⇔ x = -2,5 Vậy tập nghiệm của phương trình là S = {3;-2,5} b) (x2 - 4) + (x - 2)(3 - 2x) = 0 ⇔ (x - 2)(x + 2) + (x - 2)(3 - 2x) = 0 ⇔ (x - 2)(x + 2 + 3 - 2x) = 0 ⇔ (x - 2)(-x + 5) = 0 ⇔ x - 2 = 0 hoặc -x + 5 = 0 1) x - 2 = 0 ⇔ x = 2 2) -x + 5 = 0 ⇔ x = 5 Vậy tập nghiệm của phương trình là S = {2;5}
Đúng 0
Bình luận (0)
a) 2x(x - 3) + 5(x - 3) = 0 ⇔ (x - 3)(2x + 5) = 0 ⇔ x - 3 = 0 hoặc 2x + 5 = 0 1) x - 3 = 0 ⇔ x = 3 2) 2x + 5 = 0 ⇔ 2x = -5 ⇔ x = -2,5 Vậy tập nghiệm của phương trình là S = {3;-2,5} b) (x2 - 4) + (x - 2)(3 - 2x) = 0 ⇔ (x - 2)(x + 2) + (x - 2)(3 - 2x) = 0 ⇔ (x - 2)(x + 2 + 3 - 2x) = 0 ⇔ (x - 2)(-x + 5) = 0 ⇔ x - 2 = 0 hoặc -x + 5 = 0 1) x - 2 = 0 ⇔ x = 2 2) -x + 5 = 0 ⇔ x = 5 Vậy tập nghiệm của phương trình là S = {2;5}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời











