x(2x – 7) – 4x + 14 = 0
⇔ x.(2x - 7) – (4x – 14) = 0
⇔ x(2x – 7) – 2(2x – 7) = 0
⇔(x – 2)(2x – 7) = 0
⇔ x – 2 = 0 hoặc 2x – 7 = 0
+ x – 2 = 0 ⇔ x = 2.
+ 2x – 7 = 0 ⇔ 2x = 7 ⇔ x = 7/2
Vậy tập nghiệm của phương trình là 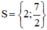
x(2x – 7) – 4x + 14 = 0
⇔ x.(2x - 7) – (4x – 14) = 0
⇔ x(2x – 7) – 2(2x – 7) = 0
⇔(x – 2)(2x – 7) = 0
⇔ x – 2 = 0 hoặc 2x – 7 = 0
+ x – 2 = 0 ⇔ x = 2.
+ 2x – 7 = 0 ⇔ 2x = 7 ⇔ x = 7/2
Vậy tập nghiệm của phương trình là 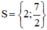
phân tích vế trái thành nhân tử, giải phương trình sau: 2x(x – 3) + 5(x – 3) = 0
Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:
a) x3 – 3x2 + 3x – 1 = 0;
b) x(2x - 7) - 4x + 14 = 0
Phân tích vế trái thành nhân tử, giải phương trình sau: (2x – 5)2 – (x + 2)2 = 0
Phân tích vế trái thành nhân tử, giải phương trình sau: (x2 – 4) + (x – 2)(3 – 2x) = 0
Bằng cách phân tích vế trái thành nhân tử, giải các PT sau:
d) \(x\left(2x-7\right)-4x+14=0\)
e) \(\left(2x-5\right)^2-\left(x+2\right)^2=0\)
f) \(x^2-x-\left(3x-3\right)=0\)
Phân tích vế trái thành nhân tử, giải phương trình sau: x2 – x – (3x – 3) = 0
Phân tích vế trái thành nhân tử, giải phương trình sau: x3 – 3x2 + 3x – 1 = 0
Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:
a) 2x(x - 3) + 5(x - 3) = 0
b) (x2 - 4) + (x - 2)(3 - 2x) = 0
Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:
a) 2x(x - 3) + 5(x - 3) = 0
b) (x2 - 4) + (x - 2)(3 - 2x) = 0