Nếu có 3 đường thẳng cắt nhau tại 1 điểm thì chúng tạo thành 6 tia chung gốc.

Mỗi tia tạo với 5 tia còn lại 5 góc mà có 6 tia như vậy nên có tất cả số góc là:

                       5 x 6 = 30 góc

Vì mỗi góc được tính lặp lại 2 lần nên có tất cả:

                       30 : 2 = 15 góc

 3 đường thẳng cắt nhau tạo thành 3 góc bẹt. Vậy có tất cả số góc khác góc bẹt là:

                        15 - 3 = 12 góc khác góc bẹt

Có tất cả 12 góc khác góc bẹt  mà mỗi góc có 1 góc đối đỉnh với nó. Nên có tất cả:

                       12 : 2 = 6 cặp góc đối đỉnh

Nguồn: https://h.vn/hoi-dap/question/87465.html

b,https://olm.vn/hoi-dap/question/181733.html

bạn click vô link sẽ dẫn đến bài viết

có 6 góc đối đỉnh

6 góc nha k mk đang âm điểm

có 3.2/2 = 3 cặp đối đỉnh

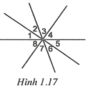
a) Liệt kê các cặp góc đối đỉnh

Ÿ Xét các cặp góc “đơn”:

Góc 1 đối đỉnh với góc 5; Góc 2 đối đỉnh với góc 6; Góc 3 đối đỉnh với góc 7; Góc 4 đối đỉnh với góc 8. Có tất cả 4 góc “đơn” đối đỉnh.

Ÿ Xét các cặp góc “ghép đôi” (ghép hai góc đơn kề nhau thành một góc “ghép đôi”):

Góc 12 đối đỉnh với góc 56; Góc 23 đối đỉnh với góc 67; Góc 34 đối đỉnh với góc 78; Góc 45 đối đỉnh với góc 81. Có tất cả 4 cặp góc “ghép đôi” đối đỉnh.

Ÿ Xét các cặp góc “ghép ba” (ghép ba góc đơn kề nhau thành một góc “ghép ba”):

Góc 123 đối đỉnh với góc 567; Góc 234 đối đỉnh với góc 678; Góc 345 đối đỉnh với góc 781; Góc 456 đối đỉnh với góc 812. Có tất cả 4 cặp góc “ghép ba” đối đỉnh.

Vậy tổng cộng có 4.3 = 12  cặp góc đối đỉnh.

b) Xây dựng công thức tính số cặp góc đối đỉnh.

Có 4 đường thẳng cắt nhau tại một điểm nên có: 4.2 = 8  (tia).

Số góc do 8 tia tạo ra là 8.7 2 = 28  (góc).

Không kể góc bẹt thì số góc còn lại là: 28 − 4 = 24  (góc).

Mỗi góc trong 24 góc này đều có một góc đối đỉnh với nó nên số cặp góc đối đỉnh được tạo thành là 24 : 2 = 12 (cặp).

* Nhận xét: Nếu có n đường thẳng cắt nhau tại một điểm thì số cặp góc đối đỉnh (không kể góc bẹt) được tạo thành là n(n-1).

Thật vậy, số tia do n đường thẳng cắt nhau tại một điểm tạo ra là 2n (tia).

Số góc do 2n tia tạo ra là: 2 n 2 n − 1 2 = n 2 n − 1 .

Không kể n góc bẹt thì số góc còn lại là: n 2 n − 1 − n = 2 n 2 − n − n = 2 n 2 − 2 n = 2 n n − 1 .

Số cặp góc đối đỉnh là: 2 n n − 1 2 = n n − 1 .

Ta có :2015(2015−1)2015(2015-1)

=2015.2014=2015.2014

=4058210

~hok tốt~

20(20-1)= 380 cặp. Công thức: n(n-1)

TL

40 góc đối đỉnh

Xin k

HT

Với n đường thẳng cắt nhau tại 1 điểm,ta được 2n tia chung gốc.

Chọn 1 tia trong 2n tia chung gốc đã cho tạo với 2n -1 tia còn lại, ta được 2n-1 (góc)

Làm như vậy với 2n tia chung gốc,ta được:

                       2n. (2n-1)      (góc)

Nhưng vì mỗi góc đã được tính 2 lần nên số góc thực có là:

                      \(\frac{2n.\left(2n-1\right)}{2}\)= n.(2n-1)   (góc)

Trong đó có n đường thẳng nên sẽ có n góc bẹt

=> Số góc khác góc bẹt là:

                    n. (2n-1) -n      (góc)

Mỗi góc trong số n.( 2n-1) -n đều có một góc đối đỉnh với nó

=> Số cặp góc đối đỉnh là: 

       \(\frac{n.\left(2n-1\right)-n}{2}\)= \(\frac{n.\left(2n-1-1\right)}{2}\)=\(\frac{n.\left(2n-2\right)}{2}\)= n.(n-1)     (cặp góc)

 Vậy có tất cả n.( n-1) cặp góc đối đỉnh được tạo thành ( không kể góc bẹt)

a) Ba đường thẳng cắt nhau tại 1 điểm tạo thành 6 tia chung gốc.

Mỗi tia tạo với 5 tia còn lại 5 góc mà có 6 tia như vậy nên có tất cả số góc là:

                       5 x 6 = 30 góc

Vì mỗi góc được tính lặp lại 2 lần nên có tất cả:

                       30 : 2 = 15 góc

 3 đường thẳng cắt nhau tạo thành 3 góc bẹt. Vậy có tất cả số góc khác góc bẹt là:

                        15 - 3 = 12 góc khác góc bẹt

Có tất cả 12 góc khác góc bẹt  mà mỗi góc có 1 góc đối đỉnh với nó. Nên có tất cả:

                       12 : 2 = 6 cặp góc đối đỉnh

b) Tương tự câu a)

b) = n(n-1) cặp

a. 6

b. n(n-1)