a) Ta có: n n − 1 = 20 b) Ta có: n n − 1 = 90
n n − 1 = 5.4 ⇒ n = 5 . n n − 1 = 10.9 ⇒ n = 10
Vậy n = 5 . Vậy n = 10 .
a) Ta có: n n − 1 = 20 b) Ta có: n n − 1 = 90
n n − 1 = 5.4 ⇒ n = 5 . n n − 1 = 10.9 ⇒ n = 10
Vậy n = 5 . Vậy n = 10 .
a) Nếu có 3 đường thẳng cắt nhau tại 1 điểm thì chúng tạo thành mấy cặp góc đối đỉnh? ( ko kể góc bẹt )
b) Nếu có n đường thẳng cắt nhau tại 1 điểm thì chúng tạo thành mấy cặp góc đối đỉnh? ( ko kể góc bẹt ) (\(n\in N\); n > hoặc bằng 2)
Cho bốn đường thẳng cắt nhau tại một điểm. Tìm số cặp góc đối đỉnh được tạo thành (không kể góc bẹt).
a) Bằng cách liệt kê;
b) Bằng cách tính toán
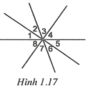
nếu có 3 đường thẳng cắt nhau tại một điểm thì chúng tạo thành mấy cặp góc đối đỉnh(khong kể góc bẹt)
Bài 1
a. Nếu 3 đường thẳng cát nhau tại một điểm thì chúng tạo thành mấy cặp góc đối đỉnh( không kể góc bẹt )?
b. Cũng hỏi như trên nếu thay 3 bằng n \(\left(n\in N;n\ge2\right)\)
Bài 2: Cho hai đường thẳng AB và CD cắt nhau tại O và tạo thành 4 góc(không kể góc bẹt)
a. Chứng minh rằng trong các góc nói trên, tồn tại hai góc có số đo nhỏ hơn hoặc bằng \(90^o\)
b. Biết tổng số đo của 3 trong 4 góc trên là \(225^o\), tính số đo của mỗi góc
Bài 3: Chúng tỏ rằng hai tia phân giác của hai góc đối đỉnh là hai tia đối nhau
Bài 4: Cho hai góc đối đỉnh. Vẽ tia phân giác của một trong hai góc đó. Chứng tỏ rằng tia đối của tia này là tia phân giác của góc còn lại
cho 4 đường thẳng cắt nhau tại 1 điểm . tìm số cặp góc đối đỉnh được tạo thành (không kể góc bẹt)
a)bằng cách liệt kê
b)bằng cách tính toán
nếu có n đường thẳng cắt nhau tại 1 điểm thì chúng tạo thành mấy góc đối đỉnh (không kể góc bẹt)
Cho 10 đường thẳng cùng đi qua 1 điểm
a, Tính số cặp góc đối đỉnh ( kể cả góc bẹt)
b, Tính số cặp góc đối đỉnh ( không kể góc bẹt)
* Từ bài toán trên hãy tổng quát lên với N đường thẳng
cho 2015 đường thẳng phân biệt cùng cắt nhau tại điểm O .hỏi các đường thẳng đó tạo thành bao nhiêu cặp góc đối đỉnh[không kể góc bẹt],làm chi tiết.
cho 20 đường thẳng cắt nhau tại điểm o hỏi có bao nhiêu cặp góc đối đỉnh ko kể góc bẹt