Cho tam giác ABC có trực tâm H.
Biểu thức A H → . H B → − H C → + B H → . H C → − H A → + C H → . H A → − H B → bằng
A. 0 →
B.0
C. A B 2 + B C 2 + C A 2
D. 1 2 A B 2 + B C 2 + C A 2
Cho tam giác ABC ,có A=60⁰; trực tâm H .Gọi M là điểm đối xứng vs H qua BC. -a) Chứng minh tam giác BHC = tâm giác BMC B) tính góc BMC
a: Ta có: M và H đối xứng nhau qua BC
nên BC là đường trung trực của MH
Suy ra: BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
Do đó: ΔBHC=ΔBMC
Bài 18. Cho tam giác ABC có AB > AC > BC và H là trực tâm. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) H là giao điểm ba đường trung trực của tam giác ABC.
b) CH vuông góc với AB.
c) AH vuông góc với BC.
. Cho tam giác ABC có Â = 60o , trực tâm H. Gọi M là điểm đối xứng với H qua BC.
a) CM : tam giác BHC+ tam giác BMC
b) Tính BMC ̂
Trong mp xOy cho tam giác ABC. bt A(3;-1) B(-1;2) I(1;-1) là trọng tâm của tam giác ABC. Trực tâm H của tam giác ABC có tọa độ (a;b). Tính a+3b
Tọa độ điểm C:
\(\left\{{}\begin{matrix}x_C=3x_I-x_A-x_B=1\\y_C=3y_I-y_A-y_B=-4\end{matrix}\right.\Rightarrow C\left(1;-4\right)\)
Ta có:
\(\overrightarrow{AH}=\left(a-3;b+1\right)\)
\(\overrightarrow{BH}=\left(a+1;b-2\right)\)
\(\overrightarrow{BC}=\left(2;-6\right)\)
\(\overrightarrow{AC}=\left(-2;-3\right)\)
Theo giả thiết
\(AH\perp BC\Rightarrow2\left(a-3\right)-6\left(b+1\right)=0\Leftrightarrow a-3b=6\left(1\right)\)
\(BH\perp AC\Rightarrow-2\left(a+1\right)-3\left(b-2\right)=0\Leftrightarrow2a+3b=4\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=\dfrac{10}{3}\\b=-\dfrac{8}{9}\end{matrix}\right.\Rightarrow a+3b=\dfrac{2}{3}\)
Cho tam giác ABC có A( -1; 3) ; B( -2; 0) và C( 5;1). Trực tâm H của tam giác ABC có toạ độ là:
A. (3 ; -1)
B. (-1 ; 3)
C. (2 ; -1)
D. (2 ; -3)
Ta có:
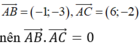
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A
Vậy H( -1 ; 3)
Chọn B.
Cho tam giác ABC có góc A= 60 độ, trực tâm H . Gọi M là điểm đối xứng với H qua BC
a, C/M tam giác BHC = tam giác BMC
b, Tính BMC
a) Vì M đối xứng với H qua BC nên BC là đường trung trực của MH
Suy ra: BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM(cmt)
CH=CM(cmt)
BC chung
Do đó: ΔBHC=ΔBMC(c-c-c)
Cho tam giác ABC có A(2,3); B(-3;4); C(1,1) xác định tọa độ trọng tâm G và trực tâm H của tam giác ABC
Cho tam giác ABC có A(-1; 1), B(3; 1), C(2; 4). Tìm tọa độ trực tâm H của tam giác ABC?
A. H( 1;1)
B. H( 1; 2)
C. (2;1)
D. (2;2)
Chọn D.
Gọi H (x; y) là trực tâm tam giác ABC nên
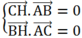
Mà
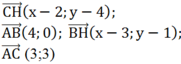
Suy ra:
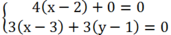
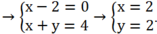
Vậy H(2; 2).
Cho tam giác ABC có trực tâm là H. M và N lần lượt là trung điểm của BC và AC. Đường trung trực BC cắt đường trung trực AC tại O.
a) Chứng minh tam giác AHB đồng dạng với tam giác MON
b) Gọi G là trực tâm tam giác ABC. Chứng minh G, H, O thẳng hàng.
a: OM//AH
ON//BH
MN//AB
=>góc BAH=góc OMN và góc ABH=góc ONM
=>ΔABH đồng dạng vơi ΔMNO
b: G là trọng tâm của ΔABC
=>GM/GA=1/2
ΔABH đồng dạng với ΔMNO nên OM/AH=MN/AB=1/2
=>OM/AH=MG/AG
=>ΔHAG đồng dạng với ΔOMG
c: ΔHAG đồng dạng với ΔOMG
=>góc AGH=góc OGM
=>H,G,O thẳng hàng