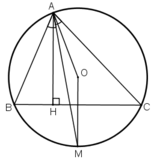
Cho tam giác ABC nội tiếp (O) đường phân giác của góc A cắt đường tròn tại P, đường cao AH (H thuộc PC)

Những câu hỏi liên quan
1, Cho tam giác nhọn ABC co H là trực tâm, gọi M,N lần lượt là trung điểm của BC và AH. Đường phân giác trong góc A cắt MN tại K. CM AK vuông góc vs HK
2, Cho tam giác ABC nội tiếp đường tròn (O), Gọi AH, AD lần lượt là đường cao, đường phan giác trong của tam giác ABC (H,D thuộc BC). Tia AD cắt (O) tại E, tia EH cắt (O) tại F vaf tia FD cắt (O) tại K. CM AK là đường kính của (O)
Từng bài 1 thôi bạn!
vẽ trên đt thông cảm!
Do đường tròn ngoại tiếp tam giác ABC có tâm là O
Ta có bổ đề: \(OM=AN=NH=\frac{1}{2}AH\)(tự chứng minh)
Vì \(\widehat{BAH}=\widehat{OAC}\)(cùng phụ với \(\widehat{ABC}\))
Mà AK là phân giác của \(\widehat{BAC}\)
=> AK là phân giác
\(\widehat{HAO}\Rightarrow\widehat{NAK}=\widehat{KAO}\)
Theo bổ đề trên ta có tứ giác ANMO là hình bình hành
=> HK//AO
=> \(\widehat{AKN}=\widehat{KAO}=\widehat{NAK}\left(cmt\right)\)
Hay tam giác NAK cân tại N mà N là trung điểm AH
=> AN=NH=NK
=> \(\Delta AHK\)vuông tại K
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn (O) và tia phân giác của góc A cắt đường tròn tại M. Vẽ đường cao AH. Chứng minh rằng:
AM là tia phân giác của góc OAH.
cho tam giác nhọn ABC nội tiếp đường tròn (O) (AB<AC).kẻ đường cao AH và đường kính AD của đường tròn O. phân giác góc BAC cắt (O) tại E. a)AH//OEb)AC ²=AM.AD
Xem chi tiết
a: AE là phân giác của góc BAC
=>EB=EC
mà OB=OC
nên OE là trung trực của BC
=>OE vuông góc BC
=>OE//AH
b: Điểm M ở đâu vậy bạn?
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O các đường cao AM , BN cho tam giác ABC cắt nhau tại H và cắt đường tròn lần lượt tại D và E Chứng minh A, tứ giác MHNC nội tiếp đường tròn B, CD = CE C, CB là tia phân giác của góc HCD
a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CED=góc CAD
góc CDE=góc CAE
mà góc CAD=góc CAE(=góc CBD)
nên góc CED=góc CDE
=>CD=CE
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn O. Tia phan giác góc BAC cắt BC tại I và đường tròn tại P. Kẻ đường kính PQ của đường tròn O. các tia phân giác góc ABC và góc ACB cắt AQ lần lượt tại E,F. chứng minh
a) PC^2=PI.PA
b) 4 điểm B,C,E,F thuộc 1 đường tròn
Cho tam giác ABC vuông tại A, đường cao AH. Tia phân giác góc BAH và góc CAH cắt BC tại D và E. Gọi O là tâm đường tròn nội tiếp của tam giác ABC.
a. Chứng minh O là tâm đường tròn ngoại tiếp tam giác ADE
b. Tính góc DOE.
cho tam giác ABC nhọn nội tiếp đường tròn tâm O.Kẻ đường cao AH cắt đường tròn tâm O tại M.Kẻ BK cắt (O)tại N
a)CMR:cung CM=cungCN
AC là đường phân giác của góc MAN
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn tâm O, bán kính R. Gọi AH, BK là đường cao của tam giác ABC (H thuộc BC; K thuộc AC). Các tia AH, BK lần lược cắt (O) tại các điểm thứ hai là D, E a)Trên hình vẽ có bao nhiêu tứ giác nội tiếp một đường tròn. Hãy chứng minh b Chứng minh rằng: góc AHC bằng Góc ADC.
a: A,E,D,B cùng thuộc (O)
=>AEDB nội tiếp
A,E,C,B cùng thuộc (O)
=>AECB nội tiếp
B,E,C,D cùng thuộc (O)
=>BECD nội tiếp
góc AHB=góc AKB=90 độ
=>AKHB nội tiếp
b: Đề sai rồi bạn
Đúng 0
Bình luận (0)
cho tam giác ABC ( AB < AC) có ba góc nhọn nội tiếp đường tròn (O). Các đường cao BD, CE của tam giác ABC cắt nhau tại H.
1. Cm tg AEDH, BCDE nội tiếp
2. Cm OA vuông góc với DE
3. Đường tròn đường kính AH cắt đt (O) tại F ( F khác A). cm các đường thẳng DE, BC, AF đồng duy
Em chỉ cần câu 3 thôi ạ, em cảm ơn