Cho đường tròn (O; R). Từ A ngoài (O), kẻ tiếp tuyến AB, và tia OA cắt (O) tại C. Biết số đo cung BC bằng 67 0 , tính số đo của O A B ^

Những câu hỏi liên quan
Cho đường tròn (O;R) và điểm A nằm bên ngoài đường tròn sao cho OA2R. Từ A kẻ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). H là giao điểm OA vad BC.a) Chứng minh OA vuông góc với BCb) Tính AB, OH và số đo góc widehat{OAB}c) M là điểm thuộc cung nhỏ BC của đường tròn (O) , tiếp tuyến của đường tròn (O) kẻ từ M cắt AB, AC lần lượt tại E và F. Tính AE+EF+FAd) Hai đoạn thẳng OE, OF lần lượt cắt đường tròn (O) tại I và J. Tính độ dài IJ theo R
Đọc tiếp
Cho đường tròn (O;R) và điểm A nằm bên ngoài đường tròn sao cho OA=2R. Từ A kẻ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). H là giao điểm OA vad BC.
a) Chứng minh OA vuông góc với BC
b) Tính AB, OH và số đo góc \(\widehat{OAB}\)
c) M là điểm thuộc cung nhỏ BC của đường tròn (O) , tiếp tuyến của đường tròn (O) kẻ từ M cắt AB, AC lần lượt tại E và F. Tính AE+EF+FA
d) Hai đoạn thẳng OE, OF lần lượt cắt đường tròn (O) tại I và J. Tính độ dài IJ theo R
Từ một điểm A nằm bên ngoài đường tròn ( O ), kẻ các tiếp tuyến AB, AC với đường tròn ( B,C là các tiếp điểm )
a) Chứng minh rằng ABOC là tứ giác nội tiếp
b)Cho bán kính đường tròn ( O ) bằng 3cm, độ dài đoạn thẳng OA bằng 5cm. Tính độ dài đoạn thẳng BC
c) Gọi ( K ) là đường tròn qua A và tiếp xúc với đường thẳng BC tạo C. Đường trknf (K) và đường tròn (O ) cắt nhau tại điểm thứ hai là M. Chứng minh rằng đường thẳng BM đi qua trung điểm của đoạn thẳng AC
Bài 1: Cho (O) dây cung AB. Tiếp tuyến tại A và B cắt nhau tại M. Biết AMB 50°a) Tính số đo cung AB.b) Trên nửa mp bờ OB (không chứa điểm A), kẻ đường thẳng d qua O và song song với BM, d cắt (O) tại D. Tính số đo cung AD.Bài 2: Cho (O;R). Một điểm A ở ngoài đường tròn sao cho OA2R. Vẽ các tiếp tuyến AB và AC đến (O) (A, B là hai tiếp điểm).a) Tính số đo các góc AOB và BOC.b) Tính số đo cung nhỏ và cung lớn BC.** VẼ HÌNH GIÙM MIK VỚI CẢM ƠN NHÌU
Đọc tiếp
Bài 1: Cho (O) dây cung AB. Tiếp tuyến tại A và B cắt nhau tại M. Biết AMB = 50°
a) Tính số đo cung AB.
b) Trên nửa mp bờ OB (không chứa điểm A), kẻ đường thẳng d qua O và song song với BM, d cắt (O) tại D. Tính số đo cung AD.
Bài 2: Cho (O;R). Một điểm A ở ngoài đường tròn sao cho OA=2R. Vẽ các tiếp tuyến AB và AC đến (O) (A, B là hai tiếp điểm).
a) Tính số đo các góc AOB và BOC.
b) Tính số đo cung nhỏ và cung lớn BC.
** VẼ HÌNH GIÙM MIK VỚI CẢM ƠN NHÌU
Cho đường tròn(O;R) và một điểm A nằm ngoài đường tròn sao cho OA = 2R. Từ A kẻ hai tiếp tuyến AB, AC tới đường tròn ( b và c là các tiếp điểm ). Tìm số đo cung lớn BC của đường tròn (O).
Bài 1: Cho (O) dây cung AB. Tiếp tuyến tại A và B cắt nhau tại M. Biết AMB 50°a) Tính số đo cung AB.b) Trên nửa mp bờ OB (không chứa điểm A), kẻ đường thẳng d qua O và song song với BM, d cắt (O) tại D. Tính số đo cung AD.Bài 2: Cho (O;R). Một điểm A ở ngoài đường tròn sao cho OA2R. Vẽ các tiếp tuyến AB và AC đến (O) (A, B là hai tiếp điểm).a) Tính số đo các góc AOB và BOC.b) Tính số đo cung nhỏ và cung lớn BC.** VẼ HÌNH GIÙM MIK VỚI CẢM ƠN NHÌU
Đọc tiếp
Bài 1: Cho (O) dây cung AB. Tiếp tuyến tại A và B cắt nhau tại M. Biết AMB = 50°
a) Tính số đo cung AB.
b) Trên nửa mp bờ OB (không chứa điểm A), kẻ đường thẳng d qua O và song song với BM, d cắt (O) tại D. Tính số đo cung AD.
Bài 2: Cho (O;R). Một điểm A ở ngoài đường tròn sao cho OA=2R. Vẽ các tiếp tuyến AB và AC đến (O) (A, B là hai tiếp điểm).
a) Tính số đo các góc AOB và BOC.
b) Tính số đo cung nhỏ và cung lớn BC.
** VẼ HÌNH GIÙM MIK VỚI CẢM ƠN NHÌU
Bài 1: Cho (O) dây cung AB. Tiếp tuyến tại A và B cắt nhau tại M. Biết AMB 50°a) Tính số đo cung AB.b) Trên nửa mp bờ OB (không chứa điểm A), kẻ đường thẳng d qua O và song song với BM, d cắt (O) tại D. Tính số đo cung AD.Bài 2: Cho (O;R). Một điểm A ở ngoài đường tròn sao cho OA2R. Vẽ các tiếp tuyến AB và AC đến (O) (A, B là hai tiếp điểm).a) Tính số đo các góc AOB và BOC.b) Tính số đo cung nhỏ và cung lớn BC.** VẼ HÌNH GIÙM MIK VỚI CẢM ƠN NHÌU
Đọc tiếp
Bài 1: Cho (O) dây cung AB. Tiếp tuyến tại A và B cắt nhau tại M. Biết AMB = 50°
a) Tính số đo cung AB.
b) Trên nửa mp bờ OB (không chứa điểm A), kẻ đường thẳng d qua O và song song với BM, d cắt (O) tại D. Tính số đo cung AD.
Bài 2: Cho (O;R). Một điểm A ở ngoài đường tròn sao cho OA=2R. Vẽ các tiếp tuyến AB và AC đến (O) (A, B là hai tiếp điểm).
a) Tính số đo các góc AOB và BOC.
b) Tính số đo cung nhỏ và cung lớn BC.
** VẼ HÌNH GIÙM MIK VỚI CẢM ƠN NHÌU
Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm).a, Tính
A
O
M
^
b, Tính
A
O
B
^
và số đo cung
A
B
⏜
nhỏc, Biết đoạn thẳng OM cắt (O)...
Đọc tiếp
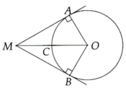
Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm).
a, Tính A O M ^
b, Tính A O B ^ và số đo cung A B ⏜ nhỏ
c, Biết đoạn thẳng OM cắt (O) tại C. Chứng minh C là điểm giữa của cung nhỏ A B ⏜
a, Sử dụng tỉ số lượng giác trong tam giác vuông ∆AMO ta tính được A O M ^ = 60 0
b, Tính được A O B ^ = 120 0 , sđ A B C ⏜ = 120 0
c, Ta có A O C ⏜ = B O C ⏜ => A C ⏜ = B C ⏜
Đúng 1
Bình luận (0)
Hai tiếp tuyến tại B và C của nửa đường tròn (O;R) cắt nhau tại A. Biết OA = R. Tính số đo của cung BC.
Hai tiếp tuyến tại B và C của nửa đường tròn (O;R) cắt nhau tại A. Biết OA = R√2. Tính số đo của cung BC.
Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: OA là tia phân giác của \(\widehat{BOC}\)(Tính chất hai tiếp tuyến cắt nhau)
Suy ra: \(\widehat{BOC}=2\cdot\widehat{BOA}\)
Xét ΔOBA vuông tại B có
\(\cos\widehat{BOA}=\dfrac{BO}{OA}=\dfrac{R}{R\sqrt{2}}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
hay \(\widehat{BOA}=45^0\)
Do đó: \(\widehat{BOC}=2\cdot\widehat{BOA}=2\cdot45^0=90^0\)
hay \(sđ\stackrel\frown{BC}=90^0\)
Vậy: \(sđ\stackrel\frown{BC}=90^0\)
Đúng 4
Bình luận (0)
Cho đường tròn (O;R) lấy điểm A nằm ngoài đường tròn sao cho OA= 2R. Qua A kẻ 2 tiếp tuyến AB, AC với đường tròn (O), (B,C là các tiếp điểm).
a) Tính số đo dóc AOB
b) Từ A kẻ đường thẳng vuông gốc với AC cắt tia OB tại M. C/m MA= MOc) Lấy I là trong điểm của OA. Chứng minh I là tâm đường tròn nội tiếp tam giác ABC.
Xem chi tiết
a) Xét \(\Delta\)AOB vuông tại B có
\(\cos\widehat{AOB}=\dfrac{OB}{OA}\)(Tỉ số lượng giác góc nhọn)
\(\Leftrightarrow\cos\widehat{AOB}=\dfrac{R}{2\cdot R}=\dfrac{1}{2}\)
hay \(\widehat{AOB}=60^0\)
Vậy: \(\widehat{AOB}=60^0\)
b) Ta có: ΔOBA vuông tại B(OB⊥BA)
nên \(\widehat{AOB}+\widehat{BAO}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BAO}=30^0\)
Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AO là tia phân giác của \(\widehat{BAC}\)(Tính chất hai tiếp tuyến cắt nhau)
⇒\(\widehat{BAO}=\widehat{CAO}\)
hay \(\widehat{CAO}=30^0\)
Ta có: \(\widehat{CAO}+\widehat{MAO}=\widehat{MAC}\)(Vì tia AO nằm giữa hai tia AM,AC)
hay \(\widehat{MAO}=60^0\)
Xét ΔMOA có
\(\widehat{MAO}=60^0\)(cmt)
\(\widehat{MOA}=60^0\)(\(\widehat{AOB}=60^0\))
Do đó: ΔMOA đều(Dấu hiệu nhận biết tam giác đều)
⇒MA=MO(đpcm)
c) Ta có: ΔOBA vuông tại B(OB⊥BA)
mà BI là đường trung tuyến ứng với cạnh huyền OA(I là trung điểm của OA)
nên \(BI=\dfrac{OA}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(AI=\dfrac{OA}{2}\)(I là trung điểm của OA)
nên BI=AI(1)
Ta có: ΔOCA vuông tại C(OC⊥CA)
mà CI là đường trung tuyến ứng với cạnh huyền OA(I là trung điểm của OA)
nên \(CI=\dfrac{OA}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(AI=\dfrac{AO}{2}\)(I là trung điểm của OA)
nên CI=AI(2)
Từ (1) và (2) suy ra IA=IB=IC
hay I là giao điểm 3 đường trung trực của ΔABC
Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: \(\widehat{BAC}=\widehat{BAO}+\widehat{CAO}\)(tia AO nằm giữa hai tia AB,AC)
hay \(\widehat{BAC}=60^0\)
Xét ΔABC có AB=AC(cmt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)(cmt)
nên ΔABC đều(Dấu hiệu nhận biết tam giác đều)
Xét ΔABC đều có I là giao điểm 3 đường trung trực của tam giác(cmt)
mà trong tam giác đều, giao điểm 3 đường trung trực cũng chính là giao điểm của 3 đường phân giác(Định lí tam giác đều)
nên I là giao điểm của 3 đường phân giác trong ΔBAC
hay I là tâm đường tròn nội tiếp ΔABC(đpcm)
Đúng 0
Bình luận (0)










