
Những câu hỏi liên quan
1.Kể tên một số bản vẽ thường dùng và công dụng của chúng.2.Nêu vị trí của hình chiếu trên bản vẽ kĩ thuật, hướng chiếu của các hình chiếu.3.Phần vật thể bị mặt phẳng cắt cắt qua được vẽ bằng nét gì? Ren nhìn thấy có đường đỉnh ren và đường giới hạn ren được vẽ bằng nét gì?4.Thế nào là hình hộp chữ nhật. Thế nào là bản vẽ kĩ thuật.GIÚP MÌNH VỚI ĐANG CẦN GẤP, CẢM ƠN !
Đọc tiếp
1.Kể tên một số bản vẽ thường dùng và công dụng của chúng.
2.Nêu vị trí của hình chiếu trên bản vẽ kĩ thuật, hướng chiếu của các hình chiếu.
3.Phần vật thể bị mặt phẳng cắt cắt qua được vẽ bằng nét gì? Ren nhìn thấy có đường đỉnh ren và đường giới hạn ren được vẽ bằng nét gì?
4.Thế nào là hình hộp chữ nhật. Thế nào là bản vẽ kĩ thuật.
GIÚP MÌNH VỚI ĐANG CẦN GẤP, CẢM ƠN !
1.Bản vẽ các khối đa diện: Đọc được hình dạng, thông số hình chiếu của các khối đa diện.
- Bản vẽ các khối xoay tròn: Đọc được hình dạng, thông số của hình chiêu các khối xoay tròn.
- Bản vẽ kĩ thuật: Trình bày thông tin kĩ thuật của sản phẩm dưới dạng các hình vẽ và các kí hiệu theo các quy tắc và thường vẽ theo tỉ lệ.
- Bản vẽ chi tiết: Dùng để chế tạo và kiểm tra chi tiết máy thể hiện chính xác hình dạng, kích thước các chi tiết để chế tạo.
- Bản vẽ lắp: Dùng để lắp ráp các chi tiết. Các kích thước trên bản vẽ lắp dùng để lắp ráp các chi tiết với nhau.
- Bản vẽ nhà: Dùng trong thiết kế, thi công, xây dựng ngôi nhà thể hiện chính xác hình dáng, kích thước các chi tiết của một ngôi nhà.
Đúng 1
Bình luận (0)
2.Hình chiếu đứng: ở góc trái bản vẽ.
+ Hình chiếu bằng: ở dưới hình chiếu đứng.
+ Hình chiếu cạnh ở bên phải hình chiếu đứng.
Đúng 1
Bình luận (0)
3.Phần vật thể bị mặt phẳng cắt cắt qua được kẻ bằng đường gạch gạch.
Ren ngoài (ren trục)
- Đường đỉnh ren và đường giới hạn ren được vẽ bằng nét liền đậm
- Đường chân ren được vẻ bằng nét liền mảnh.Vòng tròn chân ren chỉ vẽ ¾ vòng.
Ren bị che khuất
- Các đường đỉnh ren, đường chân ren và đường giới hạn ren đều vẽ bằng nét đứt
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho nửa đường tròn đường kính AB
4
5
. Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hia điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tíc...
Đọc tiếp
Cho nửa đường tròn đường kính AB = 4 5 . Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hia điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
A. V = π 5 800 5 - 928 c m 3
B. V = π 15 800 5 - 928 c m 3
C. V = π 3 800 5 - 928 c m 3
D. V = π 15 800 5 - 464 c m 3
Đáp án B.
Phương pháp: Ứng dụng tích phân để tính thể tích khối tròn xoay.
Cách giải: Gắn hệ trục tọa độ Oxy như hình vẽ:
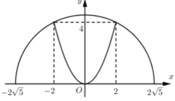
Ta có:
Phương trình đường tròn: ![]()
Phương trình parabol: ![]()
Thể tích khối cầu 
Thể tích khi quay phần tô đậm quanh trục Ox là: 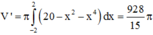
=> Thể tích cần tính 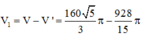
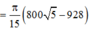
Đúng 0
Bình luận (0)
Cho nửa đường tròn đường kính
A
B
4
5
. Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hai điểm cách nhau 4 cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4 cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay quanh trục AB. Thể tích của khối tròn...
Đọc tiếp
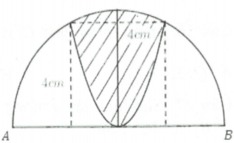
Cho nửa đường tròn đường kính A B = 4 5 . Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hai điểm cách nhau 4 cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4 cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
A. V = π 15 800 5 - 464 c m 3
B. V = π 3 800 5 - 928 c m 3
C. V = π 5 800 5 - 928 c m 3
D. V = π 15 800 5 - 928 c m 3
Cho nửa (O; R) đường kính AB. C là điểm di động trên nửa đường tròn. E à hình chiếu của C trên AB, H và K lần lượt là điểm đối xứng với E qua AC và BC, EH cắt AC tại P; EK cắt BC tại Q.
vẽ cho mình hình với
Cho nửa (O; R) đường kính AB. C là điểm di động trên nửa đường tròn. E à hình chiếu của C trên AB, H và K lần lượt là điểm đối xứng với E qua AC và BC, EH cắt AC tại P; EK cắt BC tại Q.
vẽ cho mình hình với
Trong hình cắt cục bộ, đường giới hạn phần hình cắt vẽ bằng nét:
A. Nét đứt mảnh
B. Nét gạch chấm mảnh
C. Nét lượn sóng
D. Đáp án khác
Cho nửa (O; R) đường kính AB. C là điểm di động trên nửa đường tròn. E à hình chiếu của C trên AB, H và K lần lượt là điểm đối xứng với E qua AC và BC, EH cắt AC tại P; EK cắt BC tại Q.
a.Chứng minh tứgiác EPCQ là hình chữnhật
b.Chứng minh CP.CA = CQ.CB
c.Chứng minh HK là tiếp tuyến của (O)
Cho nửa (O; R) đường kính AB. Lấy C là điểm di động trên nửa đường tròn (O). E là hình chiếu của C trên AB, H và K lần lượt là điểm đối xứng với E qua AC và BC, EH cắt AC tại P; EK cắt BC tại Q.
a.Chứng minh tứ giác EPCQ là hình chữ nhật
b.Chứng minh CP.CA = CQ.CB
c.Chứng minh HK là tiếp tuyến của (O)
a: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
DO đó: ΔCAB vuông tại C
E đối xứng H qua AC
=>AC là đường trung trực của EH
=>AC⊥EH tại trung điểm của EH
=>P là trung điểm của EH và AC⊥EH tại P
E đối xứngK qua BC
=>BC là đường trung trực của EK
=>BC⊥EK tại Q và Q là trung điểm của EK
Xét tứ giác CPEQ có \(\hat{CPE}=\hat{CQE}=\hat{PCQ}=90^0\)
nên CPEQ là hình chữ nhật
b: Xét ΔCEA vuông tại E có EP là đường cao
nên \(CP\cdot CA=CE^2\left(1\right)\)
Xét ΔCEB vuông tại E có EQ là đường cao
nên \(CQ\cdot CB=CE^2\left(2\right)\)
Từ (1),(2) suy ra \(CP\cdot CA=CQ\cdot CB\)
c: AC là đường trung trực của HE
=>AE=AH; CE=CH
CB là đường trung trực của EK
=>CE=CK; BE=BK
Xét ΔAHC và ΔAEC có
AH=AE
CH=CE
AC chung
Do đó: ΔAHC=ΔAEC
=>\(\hat{AHC}=\hat{AEC}\)
=>\(\hat{AHC}=90^0\)
=>AH⊥HC tại H
ΔAHC=ΔAEC
=>\(\hat{HCA}=\hat{ECA}\)
=>CA là phân giác của góc HCE
=>\(\hat{HCE}=2\cdot\hat{ACE}\)
Xét ΔCEB và ΔCKB có
CE=CK
BE=BK
CB chung
Do đó: ΔCEB=ΔCKB
=>\(\hat{ECB}=\hat{KCB}\)
=>CB là phân giác của góc ECK
=>\(\hat{ECK}=2\cdot\hat{ECB}\)
ΔCEB=ΔCKB
=>\(\hat{CEB}=\hat{CKB}\)
=>\(\hat{CKB}=90^0\)
=>CK⊥KB
Ta có: \(\hat{HCK}=\hat{HCE}+\hat{KCE}\)
\(=2\left(\hat{ACE}+\hat{BCE}\right)=2\cdot\hat{ACB}=2\cdot90^0=180^0\)
=>H,C,K thẳng hàng
Ta có: AH⊥HK
BK⊥KH
Do đó: AH//BK
ta có: CH=CE
CK=CE
Do đó: CH=CK
=>C là trung điểm của HK
Xét hình thang AHKB có
O,C lần lượt là trung điểm của AB,HK
=>OC là đường trung bình của hình thang AHKB
=>OC//AH//KB
=>OC⊥HK tại C
=>HK là tiếp tuyến tại C của (O)
Đúng 0
Bình luận (0)
Đường giới hạn một phần hình cắt vẽ bằng nét:
A. Nét đứt
B. Nét lượn sóng
C. Nét gạch chấm mảnh
D. Đáp án khác












