Chu kỳ của hàm số y= 10cosx là
A. k 2 π
B. 2 π 3
C. π
D. 2 π
Những câu hỏi liên quan
Chu kì của hàm số y = 2 sin ( 2 x + π / 3 ) - 3 cos ( 2 x - π / 4 ) là:
A. 2π
B. π
C. π/2
D. 4 π
Hàm số y = sin ( π / 2 - x ) + c o t x / 3 là hàm tuần hoàn với chu kì:
A. T = π.
B. T = 2π.
C. T = 3π.
D. T = 6π.
Hàm số y 1 = sin π 2 − x có chu kì T 1 = 2 π − 1 = 2 π
Hàm số y 2 = cot x 3 có chu kì T 2 = π 1 3 = 3 π
Suy ra hàm số đã cho y = y 1 + y 2 có chu kì T = B C N N 2 , 3 π = 6 π .
Vậy đáp án là D.
Đúng 0
Bình luận (0)
Hàm số y = sinx đồng biến trên đoạn nào dưới đây ?
A . [ π ; 2π ]
B . [-π ; π ]
C . [ 0 ; π ]
D . [ 0 ; \(\dfrac{\pi}{2}\)]
????????????????????
Trong các hàm số sau hàm số nào tuần hoàn với chu kỳ π ?
A. y = sin 2x
B. y = tan 2x
C. y = cos x
D. y = cot x 2
Trong các hàm số sau hàm số nào tuần hoàn với chu kỳ π ?
A. y = sin 2 x
B. y = tan 2 x
C. y = cos x
D. y = c o t x 2
Trong bốn hàm số (1)y=cos2x, (2)y=sinx, (3)y=tan2x, (4)y=cot4x có mấy hàm số tuần hoàn với chu kì là π
A. 3
B. 2
C. 0
D. 1
Cho hai điểm A, B thuộc đồ thị hàm số y sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD 2 π /3. Độ dài của cạnh BC bằng A.
2
2
B.
1
2
C. 1 D.
3
2
Đọc tiếp
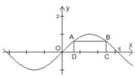
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
A. 2 2
B. 1 2
C. 1
D. 3 2
Đáp án B
Phương pháp giải:
Dựa vào đồ thị hàm số xác định hoành độ điểm D suy ra tung độ điểm A chính là độ dài BC
Lời giải: Gọi 
với 
Gọi 
thuộc đồ thị 
Vì ABCDlà hình chữ nhật 
Khi đó BC = m. Mà 
Đúng 0
Bình luận (0)
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM α, π/2 α π, A(1; 0). Gọi
M
2
là điểm đối xứng với M qua trục Ox. Số đo của cung
A
M
3
là A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
Đọc tiếp
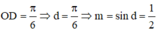
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 3 là
A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z
C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số: y = tan π / 2 – x với x ≠ k π , k ∈ Z
Đặt u = π/2 - x thì u' = -1
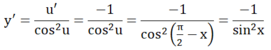
Do cos(π/2-x) = sinx
Đúng 0
Bình luận (0)