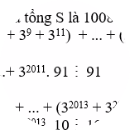chứng minh rằng:bao giờ cũng có thể chọn được hai số trong 2016 số tự nhiên khác nhau; sao cho hiệu của chúng chia hết cho 2015 (các bạn trình bày chi tiết cách giải giùm mình nha)

Những câu hỏi liên quan
chứng minh rằng trong 8 số tự nhiên khác nhau có 3 chữ số bao giờ cũng chọn được hai số khi viết liền nhau được 1 số chia hết cho 7
Chứng minh rằng trong 8 số tự nhiên khác nhau có 3 chữ số bao giờ cũng chọn được hai số khi viết liền nhau được 1 số chia hết cho 7
Chứng tỏ rằng:
a. Trong 3 số tự nhiên bất kì bao giờ cũng có thể chọn được hai số sao cho tổng của chứng chia hết cho 2.
b. Nếu hai số tự nhiên a và b (a>b) khi chia cho số tự nhiên m có cùng số dư thì a-b chia hết cho m.
c. Trong 6 số tự nhiên bất kì bao giờ cũng có thể chọn được hai số sao cho hiệu của chúng chia hết cho 5.
Chứng minh rằng trong 8 số tự nhiên có 3 chữ số bao giờ cũng chọn được hai số mà khi viết liền nhau được 1 số có 6 chữ số và chia hết cho 7
Khi chia một số cho 7 ta có thể có 7 số dư 0,1,2,3,4,5,6. Nên trong 8 số đó ta luôn chọn được 2 số khi chia cho 7 có cùng số dư.
Giả sử hai số đó là a,b đều chia cho 7 dư r . Ghép 2 số đó lại thành số có giá trị 1000.a+b hoặc 1000.b+a.
=>1000.a+b = 994a + 6a + b
=>1000.a+b ≡ 7.142.a+ 6a + b (mod 7)
=>1000.a+b ≡ 6a + b (mod 7)
=>1000.a+b ≡ 6r + r (mod 7)
=>1000.a+b ≡ 7r (mod 7)
=>1000.a+b ≡ 0 (mod 7)
=>đpcm.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng trong 8 số tự nhiên có 3 chữ số bao giờ cũng chọn được hai số mà khi viết liền nhau được 1 số có 6 chữ số và chia hết cho 7
Ta đã biết 1 số tự nhiên khi chia cho 7 chỉ có thể có 7 loại số dư là dư 0; 1; 2; 3; 4; 5; 6. Đề bài cho 8 số mà chỉ có 7 loại số dư nên theo nguyên lí Đirichlet sẽ có ít nhất 2 số cùng dư trong phép chia cho 7
Gọi 2 số đó là abc và deg (\(a;d\ne0\); a;b;c;d;e;g là các chữ số)
=> số được tạo bởi 2 số đó khi viết liền nhau là abcdeg
Ta có: abcdeg = abc.1000 + deg
= abc.1001 - abc + deg
= abc.7.143 - (abc - deg)
Do abc.7.143 chia hết cho 7; abc - deg chia hết cho 7 vì 2 số này cùng dư trong phép chia cho 7
=> abcdeg chia hết cho 7 (đpcm)
Đúng 1
Bình luận (0)
chứng minh rằng trong 27 số tự nhiên khác nhau tùy ý nhỏ hơn 100 có thể chọn được hai số có ước chung lớn nhất khác 1.
Phân hoạch \(100\) số tự nhiên đầu tiên thành các tập hợp sau:
\(A_1=\left\{1\right\}\)
\(A_2=\left\{2;4;6;8;...;100\right\}\)
\(A_3=\left\{3;9;15;...;99\right\}\)
\(A_5=\left\{5;25;35;55;...;95\right\}\)
Nghĩa là \(A_i\) với \(i\) nguyên tố chứa các bội của \(i\) mà không chia hết cho số nào nhỏ hơn \(i\) trừ số \(1\).
Giả sử có 27 số mà trong chúng không có ước chung lớn nhất khác 1.
Với mọi \(i\), trong mỗi \(A_i\) ta chỉ chọn được tối đa một số, vì nếu chọn 2 số thì chúng có ước chung là \(i\).
Có 25 số nguyên tố nhỏ hơn 100, tương ứng trong 25 \(A_i\) chỉ chọn được 25 số là tối đa.
Chọn thêm số 1 thì tối đa chọn được 26 số sao cho không có ước chung lớn nhất khác 1.
Nên nếu chọn 27 số thì trong chúng có ước chung lớn nhất khác 1.
Đúng 0
Bình luận (0)
Chứng minh rằng trong 8 số tự nhiên bất kì, mỗi số có 3 chữ số, bao giờ cũng có thể chọn được 2 số mà khi viết liền nhau ta thu được 1 số có 6 chữ số chia hết cho 7.
Xem thêm câu trả lời
Chứng minh rằng:
a,Trong 5 số tự nhiên liên tiếp khác nhau không chia hết cho 5 thì bao giờ cũng có hai số chia cho 5 cùng số dư
b,Trong 10 số tự nhiên không chia hết cho 10 thì bao giờ cũng tìm được hai số mà hiệu của chúng chia hết cho 10
Chứng minh rằng trong 92 số tự nhiên , mỗi số có ba chữ số bao giờ cũng chọn ra được hai số sao cho khi viết kề nhau ta được 1 số có 6 chữ số. CMR số có 6 chữ số này chia hết cho 91
Chia 92 số tự nhiên này cho 91, theo nguyên lý Đi - ric- lê tồn tại có 2 số có cùng số dư . Gọi 2 số đó là :abc và mnp . Ta có:
abcmnp=1000.abc+mnp=1000(91k+r)+(91q+r)
=91(1000k+q)+1001r
=91(1000k+q)+91.11r chia hết cho 91
Đúng 0
Bình luận (0)