Phương trình của đường thẳng qua điểm M(x0;y0 ) có vectơ pháp tuyến n → = a ; b là:
A. x − x 0 a = y − y 0 b
B. b x − x 0 − a y − y 0 = 0
C. a x + x 0 + b y + y 0 = 0
D. a x - x 0 + b y - y 0 = 0
Những câu hỏi liên quan
viết phương trình tổng quát của : a) đường thẳng Ox ; b) đường thẳng Oy ; c) đường thẳng đi qua M (x0,y0) và song song với Ox ; d) đường thẳng M (x0,y0) và vuông góc với Ox ; e) đường thẳng OM , với M (x0,y0) khác điểm O .
a)Phương Trình của đường thẳng ox là :y=0x+0 .
b)Phương Trình của đường thẳng oy là x=0
Đúng 0
Bình luận (0)
viết phương trình tổng quát của : a) đường thẳng Ox ; b) đường thẳng Oy ; c) đường thẳng đi qua M (x0,y0) và song song với Ox ; d) đường thẳng M (x0,y0) và vuông góc với Ox ; e) đường thẳng OM , với M (x0,y0) khác điểm O .
viết phương trình tổng quát của : a) đường thẳng Ox ; b) đường thẳng Oy ; c) đường thẳng đi qua M (x0,y0) và song song với Ox ; d) đường thẳng M (x0,y0) và vuông góc với Ox ; e) đường thẳng OM , với M (x0,y0) khác điểm O .
a. y=o
b. x=0
c. y=y0
d. x= x0
e. x* y0 - y* x0 =0
Đúng 0
Bình luận (0)
viết phương trình tổng quát của : a) đường thẳng Ox ; b) đường thẳng Oy ; c) đường thẳng đi qua M (x0,y0) và song song với Ox ; d) đường thẳng M (x0,y0) và vuông góc với Ox ; e) đường thẳng OM , với M (x0,y0) khác điểm O .
viết phương trình tổng quát của : a) đường thẳng Ox ; b) đường thẳng Oy ; c) đường thẳng đi qua M (x0,y0) và song song với Ox ; d) đường thẳng M (x0,y0) và vuông góc với Ox ; e) đường thẳng OM , với M (x0,y0) khác điểm O .
viết phương trình tổng quát của : a) đường thẳng Ox ; b) đường thẳng Oy ; c) đường thẳng đi qua M (x0,y0) và song song với Ox ; d) đường thẳng M (x0,y0) và vuông góc với Ox ; e) đường thẳng OM , với M (x0,y0) khác điểm O .
Cho đường tròn (C) có phương trình
x
−
a
2
+
y
−
b
2
R
2
và điểm
M
(
x
0
;
y
0
)
nằm bên trong đường tròn. Đường thẳng ∆...
Đọc tiếp
Cho đường tròn (C) có phương trình x − a 2 + y − b 2 = R 2 và điểm M ( x 0 ; y 0 ) nằm bên trong đường tròn. Đường thẳng ∆ qua M cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB. Phương trình của ∆ là:
A. ( a - x 0 ) ( x - x 0 ) + ( b - y 0 ) ( y - y 0 ) = 0
B. a + x 0 x − x 0 + b + y 0 y − y 0 = 0
C. ( a - x 0 ) ( x + x 0 ) + ( b - y 0 ) ( y + y 0 ) = 0
D. a + x 0 x + x 0 + b + y 0 y + y 0 = 0
Đáp án A.
Đường tròn (C) có tâm I(a;b).
Theo quan hệ vuông góc đường kính và dây cung: Nếu đường thẳng ∆ qua M cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB thì ∆ ⊥ I M tại M.
Do đó, đường thẳng ∆: đi qua M x 0 ; y 0 và nhận M I → = a - x 0 ; b - y 0 làm VTPT.
Phương trình ∆: a - x 0 x - x 0 + b - y 0 y - y 0 = 0
Đúng 0
Bình luận (0)
Đường thẳng Δ đi qua M(x0; y0) và nhận vectơ làm vectơ chỉ phương có phương trình là: A.
x
x
0
+
d
t
y
y
0
+...
Đọc tiếp
Đường thẳng Δ đi qua M(x0; y0) và nhận vectơ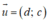 
làm vectơ chỉ phương có phương trình là:
A. x = x 0 + d t y = y 0 + c t
B. x = x 0 - c t y = y 0 + d t
C. x = x 0 + c t y = y 0 + d t
D. x = x 0 + d t y = y 0 - c t
Chọn A.
Phương trình tham số của đường thẳng Δ là:
Đúng 0
Bình luận (0)
Cho hệ phương trình
2
x
+
m
y
1
m
x
+
2
y
1
. Gọi
M
(...
Đọc tiếp
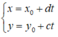
Cho hệ phương trình 2 x + m y = 1 m x + 2 y = 1 . Gọi M ( x 0 ; y 0 ) trong đó ( x 0 ; y 0 ) là nghiệm duy nhất của hệ. Phương trình đường thẳng cố định mà M chạy trên đường thẳng đó là:
A. (d): y = 2x – 1
B. (d): y = x – 1
C. (d): x = y
D. (d): y = x + 1
2 x + m y = 1 m x + 2 y = 1 ⇔ y = 1 − m x 2 2 x + m 1 − m x 2 = 1 ⇔ y = 1 − m x 2 4 − m 2 x = 2 − m ⇔ y = 1 − m x 2 2 − m 2 + m x = 2 − m
Nếu m = 2 ⇒ 0x = 0 hệ phương trình có vô số nghiệm
Nếu m = − 2 ⇒ 0x = 4 hệ phương trình vô nghiệm
Nếu m ≠ ± 2 ⇒ ( 2 + m ) x = 1 x = 1 2 + m ⇒ y = 1 2 + m ⇒ M 1 2 + m ; 1 2 + m
Nhận thấy: M có tọa độ thỏa mãn tung độ = hoành độ
M nằm trên đường thẳng (d): x = y
Đáp án:C
Đúng 0
Bình luận (0)