Cho khối chóp S. ABC có A S B ^ = B S C ^ = C S A ^ = 60 o , SA=a, SB=2a, SC=4a. Tính thể tích khối chóp S. ABC theo a.
A. 8 a 3 2 3
B. 2 a 3 2 3
C. 4 a 3 2 3
D. a 3 2 3
Những câu hỏi liên quan
Cho hình chóp S. ABC có
S
A
⊥
(
A
B
C
)
,
S
A
a
3
. Tam giác ABC vuông cân tại B, AC 2a. Thể tích khối chóp S. ABC bằng. A.
a
3
3
B.
a
3...
Đọc tiếp
Cho hình chóp S. ABC có S A ⊥ ( A B C ) , S A = a 3 . Tam giác ABC vuông cân tại B, AC = 2a. Thể tích khối chóp S. ABC bằng.
A. a 3 3
B. a 3 3 6
C. a 3 3 2
D. a 3 3 3
Cho hình chóp S. ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B, biết SA AC 2a. Tính thể tích khối chóp S. ABC A.
2
a
3
3
B.
a
3
3
C.
2
2
a
3...
Đọc tiếp
Cho hình chóp S. ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B, biết SA= AC = 2a. Tính thể tích khối chóp S. ABC
A. 2 a 3 3
B. a 3 3
C. 2 2 a 3 3
D. 4 a 3 3
Cho hình chóp tam giác đều S. ABC cạnh đáy bằng a và cạnh bên bằng b. Tính thể tích khối chóp S. ABCD. A.
a
2
3
b
2
-
a
2
4
B. ...
Đọc tiếp
Cho hình chóp tam giác đều S. ABC cạnh đáy bằng a và cạnh bên bằng b. Tính thể tích khối chóp S. ABCD.
A. a 2 3 b 2 - a 2 4
B. a 2 3 b 2 - a 2 2
C. a 2 3 b 2 - a 2 6
D. a 2 3 b 2 - a 2 12
Cho khối chóp S. ABC , có SA vuông góc với mặt đáy ABC , SA = 2a. Mặt đáy là ΔABC vuông cân tại A, có cạnh BC = 3a. Tính khối chóp S. ABC.
\(AB=AC=\dfrac{BC}{\sqrt{2}}=\dfrac{3a}{\sqrt{2}}\)
\(\Rightarrow V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.2a.\dfrac{1}{2}.\left(\dfrac{3a}{\sqrt{2}}\right)^2=\dfrac{3a^3}{2}\)
Đúng 1
Bình luận (0)
Cho khối chóp S. ABC , có mặt bên SAB là tam giác vuông cân tại S có SA = 3 cm và mặt bên SAB vuông góc với mặt đáy ABC . Mặt đáy là ΔABC vuông cân tại A. Tính khối chóp S. ABC.
Cho khối chóp S.ABC có
S
A
⊥
(
A
B
C
)
, SAa, ABa, AC2a. Tính thể tích khối chóp S. ABC.
Đọc tiếp
Cho khối chóp S.ABC có S A ⊥ ( A B C ) , SA=a, AB=a, AC=2a. Tính thể tích khối chóp S. ABC.
Cho khối chóp S. ABC có góc
A
S
B
^
B
S
C
^
C
S
A
^
60
o
và SA2, SB3, SC4. Thể tích khối chóp S. ABC. A.
2
2
B.
2...
Đọc tiếp
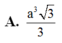
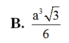
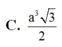
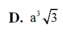
Cho khối chóp S. ABC có góc A S B ^ = B S C ^ = C S A ^ = 60 o và SA=2, SB=3, SC=4. Thể tích khối chóp S. ABC.
A. 2 2
B. 2 3
C. 4 3
D. 3 2
Chọn A
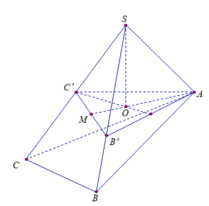
Gọi B' trên SB sao cho S B ' = 2 3 S B và C' trên SC sao cho S C ' = 2 3 S C .
Khi đó SA=SB'=SC'=2 => S. AB'C' là khối tứ diện đều.
Cách khác:
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, đỉnh S cách đều các điểm A,B,C. Biết AC 2a,BC a; góc giữa đường thẳng SB và mặt đáy (ABC) bằng
60
o
. Tính theo a thể tích V của khối chóp S.ABC? A.
V
a
6
3
4
. B. ...
Đọc tiếp
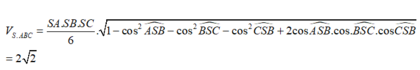
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, đỉnh S cách đều các điểm A,B,C. Biết AC = 2a,BC = a; góc giữa đường thẳng SB và mặt đáy (ABC) bằng 60 o . Tính theo a thể tích V của khối chóp S.ABC?
A. V = a 6 3 4 .
B. V = a 6 3 6 .
C. V = a 3 2 .
D. V = a 6 3 12 .
Đáp án C.
Hướng dẫn giải: Gọi H là trung điểm AC.
Do tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Đỉnh S cách đều các điểm A, B,C nên hình chiếu của S trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC
suy ra S H ⊥ ( A B C )
Tam giác vuông SBH, có
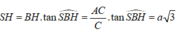
Tam giác vuông ABC ,
có A B = A C 2 - B C 2 = a 3
Diện tích tam giác vuông
S ∆ A B C = 1 2 B A . B C = a 3 2 2
Vậy V S . A B C = 1 3 S ∆ A B C . S H = a 3 2
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác vuông cận tại
B
,
AB
a
.
Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng
60
0
. Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S). A.
8
2
πa
3
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cận tại B , AB = a . Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60 0 . Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S).
A. 8 2 πa 3 3
B. 4 2 πa 3 3
C. 2 2 πa 3 3
D. 2 πa 3 3
Đáp án A
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà
Đúng 0
Bình luận (0)