Chọn A
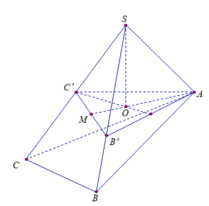
Gọi B' trên SB sao cho S B ' = 2 3 S B và C' trên SC sao cho S C ' = 2 3 S C .
Khi đó SA=SB'=SC'=2 => S. AB'C' là khối tứ diện đều.
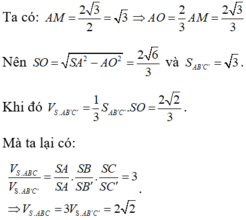
Cách khác:
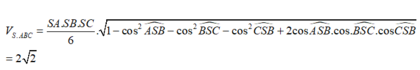
Chọn A

Gọi B' trên SB sao cho S B ' = 2 3 S B và C' trên SC sao cho S C ' = 2 3 S C .
Khi đó SA=SB'=SC'=2 => S. AB'C' là khối tứ diện đều.
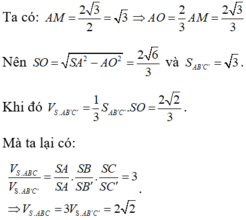
Cách khác:
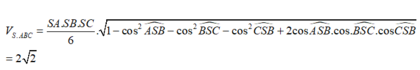
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a 2 . Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B', D', C'. Thể tích khối chóp S. AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
Cho khối chóp S. ABC có A S B ^ = B S C ^ = C S A ^ = 60 o , SA=a, SB=2a, SC=4a. Tính thể tích khối chóp S. ABC theo a.
A. 8 a 3 2 3
B. 2 a 3 2 3
C. 4 a 3 2 3
D. a 3 2 3
Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và SA=SB=SC=a. Tính thể tích của khối chóp S. ABC.
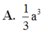
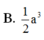
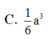
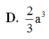
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA=a; SB=a 2 , SC=a 3 . Tính khoảng cách từ S đến mặt phẳng (ABC).
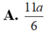
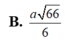
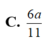
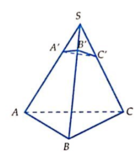
Cho khối chóp S.ABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm A', B', C' sao cho ![]() . Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S'.A'B'C'. Khi đó tỷ số
. Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S'.A'B'C'. Khi đó tỷ số ![]() là:
là:
A. 12
B. 24
C. 1 12
D. 1 24
Cho khối chóp S.ABCDS.ABCD có đáy là hình chữ nhật, AB=2a,AD=2\sqrt{3}a,SAAB=2a,AD=23a,SA vuông góc với đáy và mặt phẳng (SBC)(SBC) tạo với đáy một góc 60^o60o. Thể tích khối chóp S.ABCDS.ABCD bằng
Cho khối chóp S. ABCD có đáy ABCD là tứ giác lồi, tam giác ABD đều cạnh a, tam giác BCD cân tại C và B C D ^ = 120 0 , S A ⊥ A B C D và SA=a. Mặt phẳng (P) đi qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại M, N, P. Tính thể tích khối chóp S. AMNP.
A. a 3 3 42
B. 2 a 3 3 21
C. a 3 3 14
D. a 3 3 12
Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết V S . A E F = 1 4 V S . A B C . Tính thể tích V của khối chóp S. ABC.
A. a 3 2
B. a 3 8
C. 2 a 3 5
D. a 3 12
Cho hình chóp tam giác S. ABC có đáy ABC là tam giác đều cạnh a, SA=a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A. BCNM bằng:
A. a 3 3 12
B. a 3 3 48
C. a 3 3 24
D. a 3 3 16