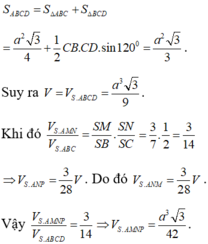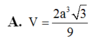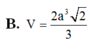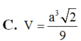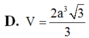Cho khối chóp S. ABCD có đáy ABCD là tứ giác lồi, tam giác ABD đều cạnh a, tam giác BCD cân tại C và B C D ^ = 120 0 , S A ⊥ A B C D và SA=a. Mặt phẳng (P) đi qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại M, N, P. Tính thể tích khối chóp S. AMNP.
A. a 3 3 42
B. 2 a 3 3 21
C. a 3 3 14
D. a 3 3 12
Chọn A
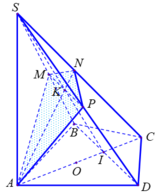
Gọi O là trọng tâm tam giác đều ABD và I là trung điểm BD thì:
Tam giác ICD vuông I có
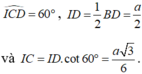
=> O và C đối xứng nhau qua đường thẳng BD
Tam giác SAC vuông tại A có SN. SC=SA²
Tam giác ABC có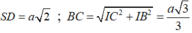 
và AC²=AB²+BC²
=> tam giác ABC vuông tại B 
Lại có tam giác SAB vuông nên 
M là trung điểm SB
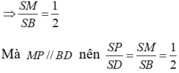
Mặt khác
