Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc.
Khằng định nào sau đây đúng?
A. AB ⊥ (ACD).
B. BC ⊥ (ACD).
C. CD ⊥ (ABC).
D. AD ⊥ (BCD).
Những câu hỏi liên quan
Cho tứ diện ABCD có (ACD)
⊥
(BCD), AC AD BC BD a và CD 2x.Với giá trị nào của x thì (ABC)
⊥
(ABD)? A.
x
a
3
3
B.
x
a
3
C. x a D.
x...
Đọc tiếp
Cho tứ diện ABCD có (ACD) ⊥ (BCD), AC = AD = BC = BD = a và CD = 2x.Với giá trị nào của x thì (ABC) ⊥ (ABD)?
A. x = a 3 3
B. x = a 3
C. x = a
D. x = a 3
Đáp án A
Phương pháp:
Xác định góc giữa hai mặt phẳng (ABC); (ABD), tìm điều kiện của x để góc đó bằng 900
Cách giải:
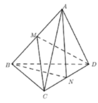
Gọi M là trung điểm của AB ta có :
Tam giác ABC cân tại C => CM ⊥ AB
Tam giác ABD cân tại D => DM ⊥ AB
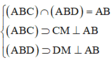
Để 
vuông tại M
Gọi N là trung điểm của CD, chứng minh tương tự như trên ta có:
Xét tam giác vuông ANC có:
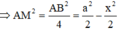
Xét tam giác vuông ACM có: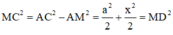 
Để ∆CDM vuông tại M 
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có ABAD
a
2
, BCBDa, CACDx. Khoảng cách từ B đến mặt phẳng (ACD) bằng
a
3
2
. Biết thể tích của khối tứ diện bằng
a
3
3
12
. Góc giữa hai mặt phẳng (ACD) và (BCD) là A.
60
o...
Đọc tiếp
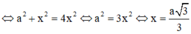
Cho tứ diện ABCD có AB=AD= a 2 , BC=BD=a, CA=CD=x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A. 60 o
B. 45 o
C. 90 o
D. 120 o
Cho tứ diện ABCD có
A
B
A
D
a
2
,
B
C
B
D
a
và
C
A
C
D
x
. Khoảng cách từ B đến mặt phẳng (ACD) bằng
a
3
2
. Biết thể tích của khối tứ diện bằng
a...
Đọc tiếp
Cho tứ diện ABCD có A B = A D = a 2 , B C = B D = a và C A = C D = x . Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A. 60 0 .
B. 45 0 .
C. 90 0 .
D. 120 0 .
Đáp án C
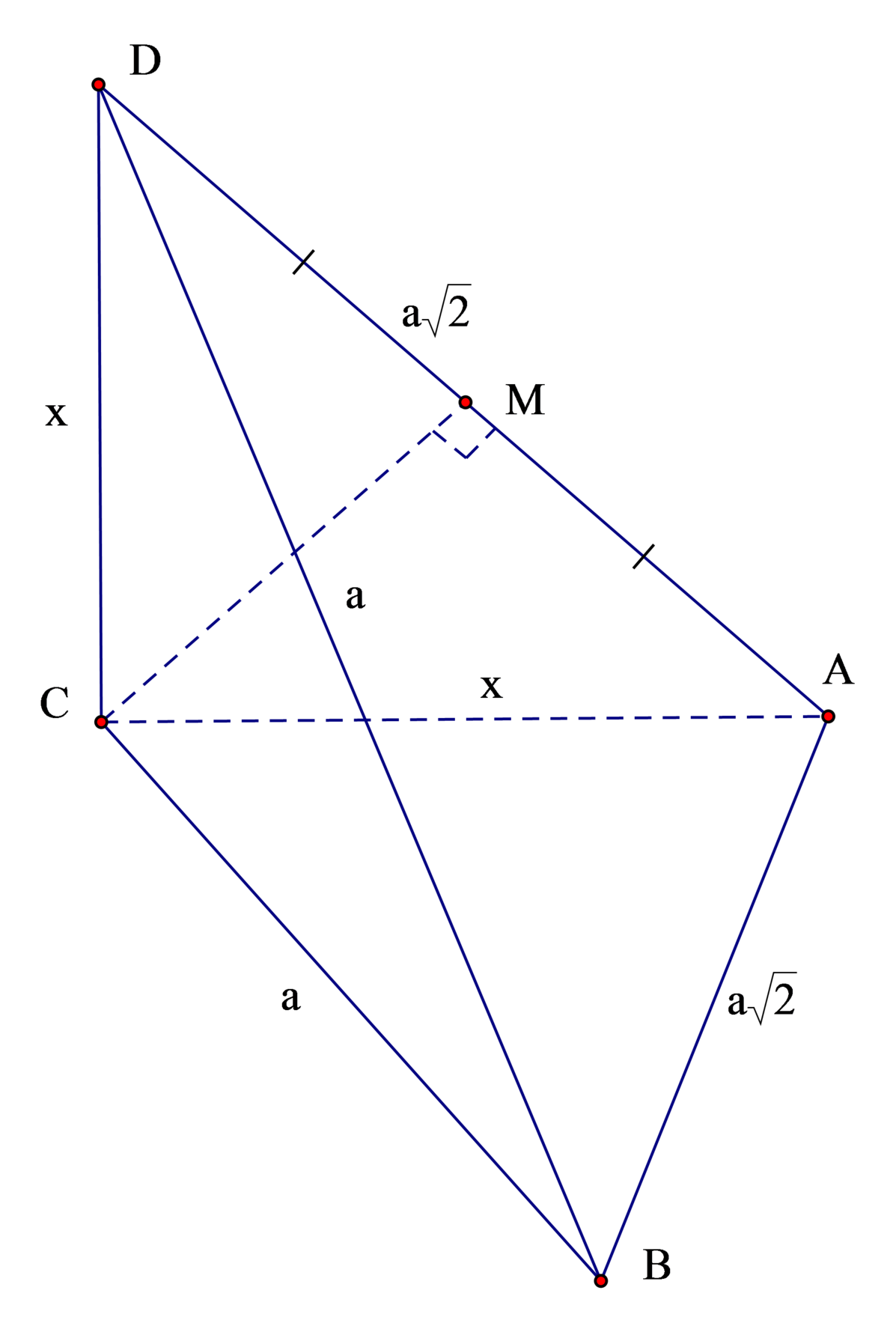
Gọi h là khoảng cách từ B → A C D
⇒ h = a 3 2 ⇒ S Δ A C D = 3 V A B C D h = 3 a 3 3 12 a 3 2 = a 2 2
Gọi M là trung điểm AD ⇒ C M ⊥ A D .
⇒ C M = 2 S A C D A D = 2. a 2 2 a 2 = a 2 2 = 1 2 A D
⇒ Δ A C D vuông tại C ⇒ C A = C D = a
Δ C A D = Δ C B A C . C . C ⇒ A C D ^ = A C B ^ = 90 0
⇒ A C ⊥ C D A C ⊥ C B ⇒ A C ⊥ B C D ⇒ A C D ⊥ B C D
Hay góc giữa hai mặt phẳng bằng 90 0
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
B
C
C
D
B
D
2
a
,
A
C
A
D
a
2
,
A
B
a
. Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là: A.
90
°
B.
60
°
C.
45
°
D.
30
°
Đọc tiếp
Cho tứ diện ABCD có B C = C D = B D = 2 a , A C = A D = a 2 , A B = a . Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là:
A. 90 °
B. 60 °
C. 45 °
D. 30 °
Cho tứ diện ABCD có BC CD BD 2a, AC AD
2
, AB a. Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là: A.
90
o
. B.
60
o
. C.
45
o
D.
30
o
Đọc tiếp
Cho tứ diện ABCD có BC = CD = BD = 2a, AC = AD = 2 , AB = a. Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là:
A. 90 o .
B. 60 o .
C. 45 o
D. 30 o
Đáp án D
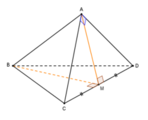
nên ∆ BCDlà tam giác đều.
nên theo định lý Py-ta-go đảo, ta có ∆ ACD vuông cân tại A .
Khi đó, gọi M là trung điểm CD thì: AM ⊥ CD và BM ⊥ CD Ta có:
∆
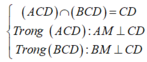
BCD đều có đường cao
∆
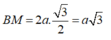
ACD vuông cân tại A nên trung tuyến
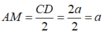
Áp dụng định lý hàm cos trong
∆
AMB, ta có:
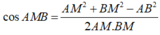
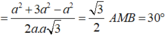
Vậy góc giữa hai mặt phẳng (ACD) và (BCD) có số đo bằng 30 o
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AB AD a
2
, BC BD a và CA CD x. Khoảng cách từ B đến mặt phẳng (ACD) bằng
a
3
2
. Biết thể tích của khối tứ diện bằng
a
3
3
12
. Góc giữa hai mặt phẳng (ACD) và (BCD) là: A.600 B.450 C.900 D.1200
Đọc tiếp
Cho tứ diện ABCD có AB = AD = a 2 , BC = BD = a và CA = CD = x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là:
A.600
B.450
C.900
D.1200
Chọn C
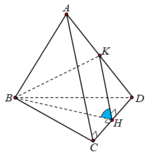
Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
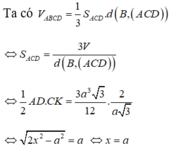
Tam giác ACD có CA=CD=x=a ; AD = a 2 => tam giác ACD vuông cân tại C
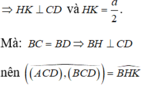
Mặt khác:
Tam giác ABD có:
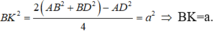
Tam giác BHK có:
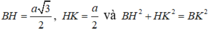
=> Tam giác BHK vuông tại H ⇒ B H K ^ = 90 o hay A C D , B C D ^ = 90 o
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
A
C
A
D
B
C
B
D
a
,
A
C
D
⊥
B
C
D
v
à
A
B
C
⊥
A
B...
Đọc tiếp
Cho tứ diện ABCD có A C = A D = B C = B D = a , A C D ⊥ B C D v à A B C ⊥ A B D . Tính độ dài cạnh CD.
A. 2 3 3 a
B. 2 2 a
C. 2 a
D. 3 3 a
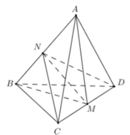
Gọi M, N lần lượt là trung điểm của CD, AB.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có (ACD)
⊥
(BCD), AC AD BC BD a, CD 2x . Giá trị của x để hai mặt phẳng (ABC) và (ABD) vuông góc với nhau là: A.
a
2
3
B.
a
3
3
C.
a
3
2
D....
Đọc tiếp
Cho tứ diện ABCD có (ACD) ⊥ (BCD), AC = AD = BC = BD = a, CD = 2x . Giá trị của x để hai mặt phẳng (ABC) và (ABD) vuông góc với nhau là:
A. a 2 3
B. a 3 3
C. a 3 2
D. a 5 3
Phương pháp:
Xác định góc giữa hai mặt phẳng 
- Tìm giao tuyến 
- Xác định 1 mặt phẳng 
- Tìm các giao tuyến 
- Góc giữa hai mặt phẳng 
Cách giải:
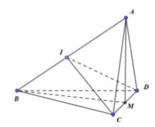
Gọi M là trung điểm của CD.
Do tam giác ACD và BCD là các tam giác cân tại A, B
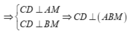
và 
Dễ dàng chứng minh được 
tại I
suy ra 
Lại có: 
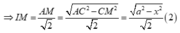
Từ (1), (2) suy ra: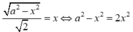 
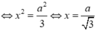
Chọn: B
Đúng 0
Bình luận (0)
cho tứ diện ABCD và điểm M nằm trong tứ diện, qua M dựng các mặt phẳng (a) song song (BCD), (b) song song (ACD), (c) song song (ABD), (d) song song (ABC). Biết (a) cắt AB tại E, (b) cắt BC tại F, (c) cắt CD tại P, (d) cắt AD tại Q
cmr: \(\sqrt{\dfrac{EA}{EB}}+\sqrt{\dfrac{FB}{FC}}+\sqrt{\dfrac{PC}{PD}}+\sqrt{\dfrac{QD}{QA}}\ge4\sqrt{3}\)