Phương án A sai vì chỉ có AB ⊥ CD; phương án B sai vì chỉ có : BC ⊥ CD
Phương án C đúng vì
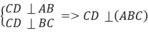
Phương án D sai vì AD không vuông góc với đường thẳng nào thuộc mặt phẳng (BCD)
Đáp án C
Phương án A sai vì chỉ có AB ⊥ CD; phương án B sai vì chỉ có : BC ⊥ CD
Phương án C đúng vì
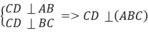
Phương án D sai vì AD không vuông góc với đường thẳng nào thuộc mặt phẳng (BCD)
Đáp án C
Cho tứ diện ABCD có AB=AD= a 2 , BC=BD=a, CA=CD=x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A. 60 o
B. 45 o
C. 90 o
D. 120 o
Cho tứ diện ABCD có BC = CD = BD = 2a, AC = AD = 2 , AB = a. Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là:
A. 90 o .
B. 60 o .
C. 45 o
D. 30 o
cho tứ diện ABCD và điểm M nằm trong tứ diện, qua M dựng các mặt phẳng (a) song song (BCD), (b) song song (ACD), (c) song song (ABD), (d) song song (ABC). Biết (a) cắt AB tại E, (b) cắt BC tại F, (c) cắt CD tại P, (d) cắt AD tại Q
cmr: \(\sqrt{\dfrac{EA}{EB}}+\sqrt{\dfrac{FB}{FC}}+\sqrt{\dfrac{PC}{PD}}+\sqrt{\dfrac{QD}{QA}}\ge4\sqrt{3}\)
Cho khối tứ diện ABCD có BC=3, CD=4, ABC ⏜ = B C D ⏜ = A D C ⏜ = 90 o C Góc giữa hai đường thẳng AD và BC bằng 60 o C Côsin góc giữa hai mặt phẳng (ABC) và (ACD) bằng
A. 2 43 43
B. 43 86
C. 2 43 43
D. 43 43
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Điểm cách đều bốn điểm A, B, C, D là:
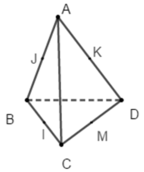
A. trung điểm J của AB
B. trung điểm I của BC
C. trung điểm K của AD
D. trung điểm M của CD
cho hình tứ diện ABCD có AB,AC,AD đôi một vuông góc và AB=AC=AD=5cm gọi M là trung điểm BC a) chứng minh BC vuông góc ADM b) tính khoảng cách từ điểm A đén BCD C) tính góc giữa đường thẳng DM và mặt phẳng ABC
Cho tứ diện ABCD có hai mặt ABC và ADC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác ABC vuông tại A có AB =a, AC =b. Tam giác ACD vuông tại D có CD = a.
a) Chứng minh các tam giác BAD và BDC là các tam giác vuông.
b) Gọi I và K lần lượt là trung điểm của AD và BC. Chứng minh IK là đường vuông góc chung của hai đường thẳng AD và BC.
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc.
Mặt phẳng (ABD) vuông góc với mặt phẳng nào của tứ diện?
A. Không vuông góc với mặt nào?
B. (ACD)
C. (ABC)
D. (BCD)
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Chứng minh: Góc giữa hai mặt phẳng (ACD) và (BCD) là A I B ^