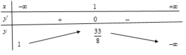
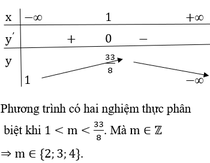
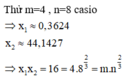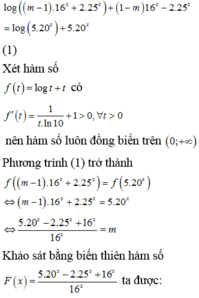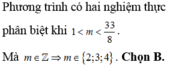Cho m, n là các số nguyên dương khác 1. Gọi P là tích các nghiệm của phương trình 2018 log m x log n x = 2017 log m x + 2018 log n x + 2019 . P nguyên và đạt giá trị nhỏ nhất khi:
A. m . n = 2 2020 .
B. m . n = 2 2017 .
C. m . n = 2 2019 .
D. m . n = 2 2018 .