Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn 1 cái bút và 1 quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A. 80.
B. 70.
C. 90.
D. 60.
Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn 1 cái bút và 1 quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A. 80.
B. 60
C. 90.
D. 70
Đáp án: A
Vì 10.8=80 .Vậy bạn học sinh đó có 80 cách chọn
lớp 5a có một số sách và bút chì làm phần thưởng cho học sinh giỏi, đặt trên 1 quyển sách 1 cái bút thì còn 38 cái không có chỗ đặt. sau khi tặng cho mỗi em 6 bút chì và 3 quyển sách. thì thừa 6 bút chì và 4 quyển sách. hỏi
a, lơp có bao nhiêu học sinh giỏi ?
b, cô giáo có bao nhiêu bút chì và bao nhiêu sách ?
mình cần câu trả lời ngay
Lớp 5A có một số sách và bút chì làm phần thưởng cho học sinh giỏi. Đặt trên 1 quyển sách 1 cái bút thì còn 38 cái không có chỗ đặt. Sau khi tặng cho mỗi em 6 bút chỉ và 3 quyển sách thì còn thừa 6 bút chì và 4 quyển sách. Hỏi:
a) Lớp có bao nhiêu học sinh giỏi?
b) Cô giáo có bao nhiêu bút chì và bao nhiêu sách?
Có 8 cái bút khác nhau và 7 quyển vở khác nhau được gói trong 15 hộp. Một học sinh được chọn bất kì hai hộp. Xác suất để học sinh đó chọn được một cặp bút và vở là
A. 8 15
B. 8 105
C. 1 15
D. 1 7
Đáp án A
Xác suất cần tính là C 8 1 C 7 1 C 15 2 = 8 15
Trên một kệ sách có 6 quyển sách toán khác nhau, 7 quyển sách lý khác nhau và 8 quyển sách hóa khác nhau. Có bao nhiêu cách chọn 4 quyển sách khác nhau đủ cả ba loại sách toán, lý và hóa tặng cho 4 học sinh của lớp 11A1?
Lời giải:
Chọn 4 quyển sách khác nhau đủ 3 loại, có các TH sau:
TH1: 1 toán, 1 lý, 2 hóa: $A_1=C^1_6.C^1_7.C^2_8$ cách
TH2: 2 toán, 1 lý, 1 hóa: $A_2=C^2_6.C^1_7.C^1_8$ cách
TH3: 1 toán, 2 lý, 1 hóa: $A_3=C^1_6.C^2_7.C^1_8$ cách
Tổng số cách: $A_1+A_2+A_3=3024$ cách
Một bạn học sinh có 3 cái quần khác nhau và 2 cái áo khác nhau. Hỏi bạn học sinh đó có bao nhiêu cách lựa chọn 1 bộ quần áo.
A. 5
B. 4
C. 3
D. 6
Chọn D.
Phương pháp:
Sử dụng quy tắc nhân.
Cách giải:
Học sinh đó có 3.2 = 6 cách lựa chọn 1 bộ quần áo.
Một bạn học sinh có 3 cái quần khác nhau và 2 cái áo khác nhau. Hỏi bạn học sinh đó có bao nhiêu cách lựa chọn 1 bộ quần áo.
![]()
![]()
![]()
![]()
Bạn Đức có 6 quyển sách Văn khác nhau và 10 quyển sách Toán khác nhau. Hỏi bạn Đức có bao nhiêu cách chọn ra 3 quyển sách trong đó có đúng 2 quyển cùng loại.
A.560
B.420
C.270
D.150
Chọn B.
TH1: 3 quyển được chọn có 2 quyển sách Văn, 1 quyển sách Toán.
Chọn 2 quyển Văn trong 6 quyển Văn khác nhau có 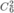 cách.
cách.
Chọn 1 quyển Toán trong 10 quyển Toán khác nhau có 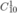 cách.
cách.
Áp dụng quy tắc nhân, có 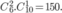
TH2: 3 quyển được chọn có 2 quyển sách Toán, 1 quyển sách Văn.
Chọn 1 quyển Văn trong 6 quyển Văn khác nhau có 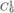 cách.
cách.
Chọn 2 quyển Toán trong 10 quyển Toán khác nhau có 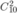 cách.
cách.
Áp dụng quy tắc nhân, có 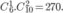
Vậy số cách chọn ra 3 quyển sách trong đó có đúng 2 quyển cùng loại là 150 + 270 = 420.
Bạn Đức có 6 quyển sách Văn khác nhau và 10 quyển sách Toán khác nhau. Hỏi bạn Đức có bao nhiêu cách chọn ra 3 quyển sách trong đó có đúng 2 quyển cùng loại.
A. 560
B. 420
C. 270
D. 150