Cho dãy số ( u n ) thỏa mãn u n + 1 = 3 u n - 2 u n - 1 và u 1 = log 2 5 , u 2 = log 2 10 . Giá trị nhỏ nhất của n để u n > 1024 + log 2 5 2 bằng
A. n=11
B. n=12
C. n=13
D. n=15
Dãy số thỏa mãn với mọi . Tính lim un
.
Cho dãy u(n) thỏa mãn log 3 u 1 2 - 3 log u 5 = log 3 u 2 + 9 - log u 1 6 và u n + 1 = u n + 3 u 1 > 0 với mọi n≥1 Đặt S n = u 1 + u 2 + . . . + u n Tìm giá trị nhỏ nhất của n để S n > 5 n 2 + 2018 2
A. 1647
B. 1650
C. 1648
D. 1165
Cho dãy số u n thỏa mãn u 1 = 2018 ; u n + 1 = u n + n 2 với n. Có bao nhiêu số nguyên dương n thỏa mãn u n ≤ 330368
A. 2017.
B. 100.
C. 101.
D. 2018.
Cho dãy (un) thỏa mãn: \(\left\{{}\begin{matrix}u_1=5\\u_{n+1}=\dfrac{u^{2022}_n+3.u_n+16}{u_n^{2021}-u_n+11}\end{matrix}\right.\), ∀nϵN*
CMR (un) tăng
Xét hàm số \(f\left(x\right)=\dfrac{x^{2022}+3x+16}{x^{2021}-x+11}\), ta cần cm
\(f\left(x\right)\ge x\) (*)
Thật vậy, (*) \(\Leftrightarrow x^{2022}+3x+16\ge x^{2022}-x^2+11x\)
\(\Leftrightarrow x^2-8x+16\ge0\)
\(\Leftrightarrow\left(x-4\right)^2\ge0\) (luôn đúng)
Vậy \(f\left(x\right)\ge x,\forall x\)
\(\Rightarrow u_{n+1}=f\left(u_n\right)\ge u_n\) nên \(\left(u_n\right)\) là dãy tăng.
Cho dãy số u n thỏa mãn u 1 = 2 3 và u n + 1 = u n 2 2 n + 1 u n + 1 n ≥ 1 . Tìm số nguyên dương n nhỏ nhất thỏa mãn log 1 2 u n > 12 , 3 .
A. n=50
B. n=60
C. n=51
D. n=61
cho dãy số (un) thỏa mãn: \(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=\dfrac{n\left(u_n+2\right)+n^2+1}{n+1}\end{matrix}\right.\)
tìm số hạng tổng quát của dãy số
\(u_{n+1}=\dfrac{n\left(u_n+2\right)+n^2+1}{n+1}\)
\(\Rightarrow\left(n+1\right)u_{n+1}=nu_n+n^2+2n+1\)
\(\Rightarrow\left(n+1\right)u_{n+1}-\dfrac{1}{3}\left(n+1\right)^3-\dfrac{1}{2}\left(n+1\right)^2-\dfrac{1}{6}\left(n+1\right)=n.u_n-\dfrac{1}{3}n^3-\dfrac{1}{2}n^2-\dfrac{1}{6}n\)
Đặt \(v_n=u.u_n-\dfrac{1}{3}n^3-\dfrac{1}{2}n^2-\dfrac{1}{6}n\Rightarrow\left\{{}\begin{matrix}v_1=1-\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{1}{6}=0\\v_{n+1}=v_n=...=v_1=0\end{matrix}\right.\)
\(\Rightarrow n.u_n-\dfrac{1}{3}n^3-\dfrac{1}{2}n^2-\dfrac{1}{6}n=0\)
\(\Rightarrow u_n=\dfrac{1}{3}n^2+\dfrac{1}{2}n+\dfrac{1}{6}=\dfrac{\left(n+1\right)\left(2n+1\right)}{6}\)
Cho dãy số u n thỏa mãn u n = u n - 1 + 6 , ∀ n ≥ 2 và log 2 u 5 + log 2 u 9 + 8 = 11 . Đặt S n = u 1 + u 2 + . . . + u n . Tìm số tự nhiên n nhỏ nhất thỏa mãn S n ≥ 2 5 .
A. 5
B. 4
C. 3
D. 7
Cho dãy số u n thỏa mãn u n = u n − 1 + 6 , ∀ n ≥ 2 và log 2 u 5 + log 2 u 9 + 8 = 11. Đặt S n = u 1 + u 2 + ... + u n . Tìm số tự nhiên n nhỏ nhất thỏa mãn S n ≥ 20172018.
A. 2587
B. 2590
C. 2593
D. 2584
Cho dãy số u n thỏa mãn u n = u n - 1 + 6 , ∀ n ⩾ 2 và log 2 u 5 + log 2 u 9 + 8 = 11 . Đặt S n = u 1 + u 2 + . . . + u n . Tìm số tự nhiên n nhỏ nhất thỏa mãn S n ⩾ 20172018 .
A. 2587.
B. 2590.
C. 2593.
D. 2584.
Cho dãy số ( u n ) thỏa mãn u n = u n - 1 + 6 , ∀ n ≥ 2 và log 2 u 5 + log 2 u 9 + 8 = 11 . Đặt S n = u 1 + u 2 + . . . + u n . Tìm số tự nhiên n nhỏ nhất thỏa mãn S n ≥ 2 5 .
A. 5
B. 4
C. 3
D. 7
Chọn C
Phương pháp: Dễ thấy u n = u n - 1 + 6 , ∀ n ≥ 2 suy ra dãy số đã cho là cấp số cộng công sai bằng 6.
Vậy ta cần tìm số hạng đầu.
Cách giải: Ta có
log 2 u 5 + log 2 u 9 + 8 = 11
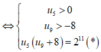
![]()
![]()
V ậ y u 1 = u 5 - 4 . 6 = 8
Do đó:
S n = u 1 + u 2 + . . + u n
= n u 1 + n ( n - 1 ) 2 d
= 3 n 2 + 5 n
⇔ 3 n 2 + 5 n - 32 > 0
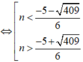
Vậy số tự nhiên n nhỏ nhất thỏa mãn S n ≥ 2 5 là 3.