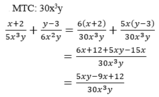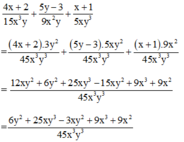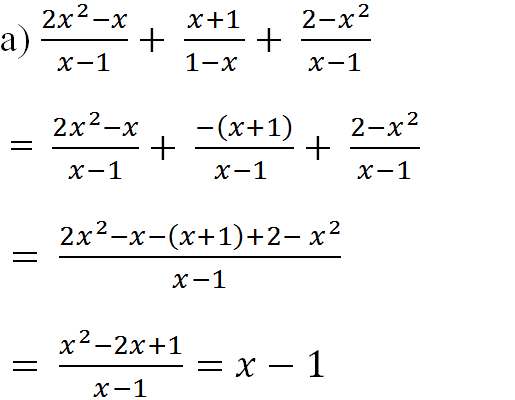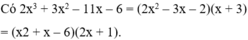Cộng các phân thức khác mẫu thức: x 3 + 2 x x 3 + 1 + 2 x x 2 - x + 1 + 1 x + 1

Những câu hỏi liên quan
Phát biểu quy tắc : cộng hai phân thức cùng mẫu thức, cộng hai phân thức khác mẫu thức.
Làm tính cộng :
\(\dfrac{3x}{x^3-1}+\dfrac{x-1}{x^2+x+1}\)
- Muốn cộng hai phân thức cùng mẫu, ta cộng các tử với nhau và giữ nguyên mẫu.
- Muốn cộng hai phân thức khác mẫu, ta quy đồng mẫu thức rồi cộng các phân thức cùng mẫu vừa tìm được.
\(\dfrac{3x}{x^3-1}+\dfrac{x-1}{x^2+x+1}\)
\(=\dfrac{3x}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{\left(x-1\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{3x+x^2-2x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{1}{x-1}\)
Đúng 0
Bình luận (0)
Cộng các phân thức khác mẫu thức: x + 2 5 x 3 y + y - 3 6 x 2 y
Cộng các phân thức khác mẫu thức:
4
x
+
2
15
x
3
y
+
5
y
-
3
9
x
2
y
+
x
+
1
5
x...
Đọc tiếp
Cộng các phân thức khác mẫu thức: 4 x + 2 15 x 3 y + 5 y - 3 9 x 2 y + x + 1 5 x y 3
Biến đổi phân thức x^2-7/4x+3 với x khác -3/4 và x khác 0 thành 1 phần thức bằng nó và có mẫu thức B=12x^2+9x
Áp dụng quy tắc đổi dấu để các phân thức có cùng mẫu thức rồi làm tính cộng phân thức :
a) \(\dfrac{2x^2-x}{x-1}+\dfrac{x+1}{1-x}+\dfrac{2-x^2}{x-1}\)
b) \(\dfrac{4-x^2}{x-3}+\dfrac{2x-2x^2}{3-x}+\dfrac{5-4x}{x-3}\)
Cho các phân thức
x
−
3
2
x
2
−
3
x
−
2
và
2
x
−
1
x
2
+
x...
Đọc tiếp
Cho các phân thức x − 3 2 x 2 − 3 x − 2 và 2 x − 1 x 2 + x − 6 với x ≠ − 3 ; x ≠ − 1 2 và x ≠ 2 . Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là N = 2 x 3 + 3 x 2 − 11 x − 6 .
Cho đa thức
A
2
x
3
+
x
2
−
13
x
+
6
và hai phân thức:
x
2
x
2
+
5
x
−
3
,
x
+
2...
Đọc tiếp
Cho đa thức A = 2 x 3 + x 2 − 13 x + 6 và hai phân thức: x 2 x 2 + 5 x − 3 , x + 2 x 2 + x − 6 với x ≠ − 3 ; x ≠ 1 2 và x ≠ 2 .
a) Chia đa thức A lần lượt cho các mẫu thức của hai phân thức đã cho.
b) Quy đồng mẫu thức của hai phân thức đã cho.
Cộng các phân thức khác mẫu thức :
a) \(\dfrac{5}{6x^2y}+\dfrac{7}{12xy^2}+\dfrac{11}{18xy}\)
b) \(\dfrac{4x+2}{15x^3y}+\dfrac{5y-3}{9x^2y}+\dfrac{x+1}{5xy^3}\)
c) \(\dfrac{3}{2x}+\dfrac{3x-3}{2x-1}+\dfrac{2x^2+1}{4x^2-2x}\)
d) \(\dfrac{x^3+2x}{x^3+1}+\dfrac{2x}{x^2-x+1}+\dfrac{1}{x+1}\)
Phát biểu các qui tắc: Cộng hai phân thức cùng mẫu thức, cộng hai phân thức khác mẫu thức. Làm tính cộng:
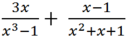
- Qui tắc cộng hai phân thức cùng mẫu:
Muốn cộng hai phân thức có cùng mẫu thức, ta cộng các tử thức với nhau và giữ nguyên mẫu thức.
- Qui tắc cộng hai phân thức khác mẫu:
Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.
- Làm tính cộng:
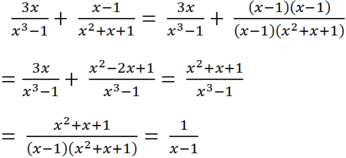
Đúng 0
Bình luận (0)