Tính tích x.y, biết rằng x và y thỏa mãn các đẳng thức sau (a, b là các hằng số): 4 a 2 - 9 x = 4 a + 4 ; với a ≠ ± 3/2 và 3 a 3 + 3 y = 6 a 2 + 9 a với a ≠ - 1

Những câu hỏi liên quan
Tính tích x.y, biết rằng x và y thỏa mãn các đẳng thức sau (a, b là các hằng số):
2
a
3
-
2
b
3
x
-
3
b
3
a
; với a
≠
b và
6
a
+
6
b...
Đọc tiếp
Tính tích x.y, biết rằng x và y thỏa mãn các đẳng thức sau (a, b là các hằng số): 2 a 3 - 2 b 3 x - 3 b = 3 a ; với a ≠ b và 6 a + 6 b y = a - b 2 với a ≠ - b
Vì a
≠
b nên
2
a
3
-
2
b
3
≠
0. Suy ra: 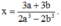
Vì a
≠
- b nên a + b
≠
0. Suy ra: 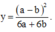
Vậy 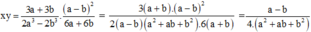
Đúng 0
Bình luận (0)
Tìm tích x*y, biết rằng x, y thỏa mãn các đẳng thức sau (a, b là hằng số): (2a^3-2b^3)x-3b=3a với a khác b và (6a+6b)y=(a-b)^2 với a khác -b.
Cho các số nguyên dương a,b,x,y thỏa mãn các đẳng thức: a+b=x+y ; a.b-a=x.y. Chứng tỏ rằng x khác y
tìm các số x y biết rằng chúng thỏa mãn các đẳng thức sau:
a> x^3 + y^3 = 152 ; x^2 - xy +y^2=19 ; x-y =2
b> x+y = 2 ; x^2+y^2=20 tính x^3+y^3
Cho a, b là các hằng số dương x và y tùy ý thuộc R thỏa mãn
x^2+y^2=1 và x^4/a + y^4/b = 1/a+b
Tính giá trị biểu thức M= x^2012/a^1004 + y^2012/b^1006 theo a và b
Ta có:
\(\frac{x^4}{a}+\frac{y^4}{b}\ge\frac{\left(x^2+y^2\right)^2}{a+b}=\frac{1}{a+b}\)
Dấu = xảy ra khi .... Làm tiếp nhé
Đúng 0
Bình luận (0)
ta có: \(\frac{x^4}{a}+\frac{y^4}{b}=\frac{1}{a+b}\)=> \(\frac{bx^4+ay^4}{ab}=\frac{\left(x^2+y^2\right)^2}{a+b}\) (vì x^2 +y^2 =1)
=>\(abx^4+b^2x^4+aby^4+a^2y^4\) = \(ab\left(x^4+2x^2y^2+y^4\right)\)
=>\(abx^4+b^2x^4+aby^4+a^2y^4\) = \(abx^4+2abx^2y^2+aby^4\)
=> \(b^2x^4-2abx^2y^2+a^2y^4=0\)
=>\(\left(bx^2-ay^2\right)^2=0\)=>\(bx^2=ay^2\Rightarrow\frac{x^2}{a}=\frac{y^2}{b}=\frac{x^2+y^2}{a+b}=\frac{1}{a+b}\)
=> \(\frac{x^{2012}}{a^{1006}}=\frac{1}{\left(a+b\right)^{1006}}\) và \(\frac{y^{2012}}{b^{1006}}=\frac{1}{\left(a+b\right)^{1006}}\)
=>\(\frac{x^{2012}}{a^{1006}}+\frac{y^{2012}}{b^{1006}}=\frac{2}{\left(a+b\right)^{1006}}\)
Đúng 0
Bình luận (0)
bài 48 nè xuân:
Kẻ DM và IN //BC (M,N thuộc AC)
ta có: ^ADM =ABC (vì DM//BC)
^AMD=^ACB (vì................)
Mà ^ABC=^ACB( vì tg ABC cân tại A) nên ^AMD=^ADM => tg ADM cân tại A=> AD=AM. mà AD=CE(gt) => AM=CE
ta có: IN//BC , mà DM//BC nên DM//IN. Mặt khác : I là t/đ của DE (gt) => N là t/đ của ME (ĐL Ta-Lét)=> MN=EN
Ta có: AN=AM+MN
CN= CE+EN
Mà AM= CE(cmt) ; MN=EN (cmt) nên AN=CN => N là t/đ của AC
Xét tg ACK có: IN//IK và N là t/đ của AC (cmt) => I là t/đ của AK (ĐL Ta -Lét)
Xét tg ADKE có: I là t/đ của AK (cmt) và I là t/đ của DE (gt)
=> tg ADKE là hbh
Đúng 0
Bình luận (0)
B1: cho a+b+c=0 và a^2+b^2+c^2=1. Tính GTBT P=a^4+b^4+c^4
B2: CMR không có các số x,y thỏa mãn hằng đẳng thức
a)2x^2+y^2-2xy+x+2=0
b)-x^2-26y^2+10xy-20y-150=0
giúp tui với ạ tui sắp phải nộp bài :<
Bài 2:
a: Ta có: \(2x^2+y^2-2xy+x+2=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{7}{4}=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}=0\left(vôlý\right)\)
b: Ta có: \(-x^2-26y^2+10xy-20y-150=0\)
\(\Leftrightarrow x^2-10xy+25y^2+y^2+20y+100+50=0\)
\(\Leftrightarrow\left(x-5y\right)^2+\left(y+10\right)^2+50=0\left(vôlý\right)\)
Đúng 1
Bình luận (0)
Bài 1:
\(a+b+c=0\Leftrightarrow\left(a+b+c\right)^2=0\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\Leftrightarrow2\left(ab+bc+ca\right)=0-1=-1\)hay \(ab+bc+ca=-\dfrac{1}{2}\Leftrightarrow\left(ab+bc+ca\right)^2=\dfrac{1}{4}\Leftrightarrow a^2b^2+b^2c^2+c^2a^2+2a^2bc+2ab^2c+2abc^2=\dfrac{1}{4}\Leftrightarrow a^2b^2+b^2c^2+c^2a^2+2abc\left(a+b+c\right)=\dfrac{1}{4}\Leftrightarrow a^2b^2+b^2c^2+c^2a^2=\dfrac{1}{4}\)Ta có: \(P=a^4+b^4+c^4=\left(a^2+b^2+c^2\right)^2-2\left(a^2b^2+b^2c^2+c^2a^2\right)=1-2.\dfrac{1}{4}=\dfrac{1}{2}\)Vậy \(P=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
chứng minh rằng các hằng đẳng thức sau thỏa mãn với mọi x, y :
a, x^2 + xy + y^2 + 1 > 0
b, x^2 + 5y^2 + 2x - 4xy -10y+ 14 >0
c, 5x^2+10y^2 - 6xy -4x -2y +3 >0
1/ Tính tổng a+b: (a+1)2+(b-2)2=4
2/ Cho x<0;y<0 biết x/2=y/3 và x2y2=576
3/ Cặp số (x;y) thỏa mãn x:(-3)=y:5 và x-y=24
4/ Tập các số hữu tỉ thỏa mãn đẳng thức x2-25x4=0
5/ Giá trị biểu thức B=x2-2xy+y2+5 khi x-y=5
1, Phân tích thành nhân tử: 8(x + y + z)^2 - (x + y)^3 - (y + z)^3 - (z + x)^32, a, Phân tích thành nhân tử: 2x^2y^2 + 2y^2z^2 + 2z^2x^2 - x^4 - y^4 - z^4b, Chứng minh rằng nếu x, y, x là ba cạnh của 1 tam giác thì A 03, Cho x, y, x là độ dài 3 cạnh của một tam giác ABC. Chứng minh rằng nếu x, y, z thỏa mãn các đẳng thức sau thì tam giác ABC là tam giác đều:a, (x + y+ z)^2 3(xy + yz + zx)b, (x + y)(y + z)(z + x) 8xyzc, (x - y)^2 + (y - z)^2 + (z - x)^2 (x + y - 2z)^2 + (y + z - 2x)^2 + (z +...
Đọc tiếp
1, Phân tích thành nhân tử: 8(x + y + z)^2 - (x + y)^3 - (y + z)^3 - (z + x)^3
2,
a, Phân tích thành nhân tử: 2x^2y^2 + 2y^2z^2 + 2z^2x^2 - x^4 - y^4 - z^4
b, Chứng minh rằng nếu x, y, x là ba cạnh của 1 tam giác thì A > 0
3, Cho x, y, x là độ dài 3 cạnh của một tam giác ABC. Chứng minh rằng nếu x, y, z thỏa mãn các đẳng thức sau thì tam giác ABC là tam giác đều:
a, (x + y+ z)^2 = 3(xy + yz + zx)
b, (x + y)(y + z)(z + x) = 8xyz
c, (x - y)^2 + (y - z)^2 + (z - x)^2 = (x + y - 2z)^2 + (y + z - 2x)^2 + (z + x - 2y)^2
d, (1 + x/z)(1 + z/y)(1 + y/x) = 8
4,
a, Cho 3 số a, b, c thỏa mãn b < c; abc < 0; a + c = 0. Hãy so sánh (a + b - c)(b + c - a)(c + a -b) và (c - b)(b - a)(a - c)
b, Cho x, y, z, t là các số nguyên dương thỏa mãn x + z = y + t; xz 1 = yt. Chứng minh y = t và x, y, z là 3 số nguyên liên tiếp
5, Chứng minh rằng mọi x, y, z thuộc Z thì giá trị của các đa thức sau là 1 số chính phương
a, A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y^4
b, B = (xy + yz + zx)^2 + (x + y + z)^2 . (x^2 + y^2 + z^2)
mày hỏi vả bài kiểm tra à thằng điên
Xem thêm câu trả lời




















