Nêu phương pháp chứng minh Mặt phẳng song song với mặt phẳng.

Những câu hỏi liên quan
Nêu phương pháp chứng minh :
- Đường thẳng song song với đường thẳng
- Đường thẳng song song với mặt phẳng
- Mặt phẳng song song với mặt phẳng
Muốn chứng minh đường thẳng a // (P), ta chứng minh đường thẳng a song song với đường thẳng b mà đường thẳng b song song với mặt phẳng (P) (a và (P) không có điểm chung)
Đúng 0
Bình luận (0)
Nêu phương pháp chứng minh Đường thẳng song song với mặt phẳng
Chứng minh đường thẳng song song với mặt phẳng
- Chứng minh d song song với đường thẳng d’ nằm trong (α) và d không thuộc(α).
- Có hai mặt phẳng song song, bất kì đường nào nằm trong hai mặt phẳng này cũng song song với mặt phẳng kia.
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Dùng phương pháp tọa độ để :
a) Chứng minh hai mặt phẳng (AB'D') và (BC'D) song song
b) Tính khoảng cách giữa hai mặt phẳng đó
Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng 1. Dùng phương pháp tọa độ để: Chứng minh hai mặt phẳng (AB’D’) và (BC’D) song song
Ta chọn hệ trục tọa độ sao cho các đỉnh của hình lập phương có tọa độ là:
A(0; 0; 0), B(1;0; 0), D(0; 1; 0)
B’(1; 0 ; 1), D’(0; 1; 1), C’ (1; 1; 1)
Phương trình của hai mặt phẳng (AB’D’) và (BC’D) là :
x + y – z = 0 và x + y – z – 1 = 0
Ta có:
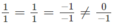
Vậy (AB’D’) // (BC’D)
Đúng 0
Bình luận (0)
Giải bài toán sau đây bằng phương pháp tọa độ :
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D cạnh bằng 1 :
a) Chứng minh rằng hai mặt phẳng (AB'D') và (BC'D) song song với nhau ?
b) Tính khoảng cách giữa hai mặt phẳng nói trên ?
giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Chứng minh hai mặt phẳng (AB'D') và (BC'D) song song.
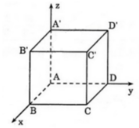
Chọn hệ trục tọa độ Oxyz có gốc O ≡ A; 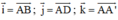
⇒ A(0; 0; 0) ; B(1; 0; 0); C(1; 1; 0); D(0; 1; 0).
A’(0; 0; 1); B’(1; 0; 1); C’(1; 1; 1); D’(0; 1; 1).
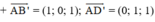
⇒ Vectơ pháp tuyến của (AB’D’) là:
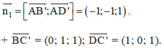
⇒ Vectơ pháp tuyến của (BC’D) là:
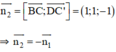
⇒ (AB’D’) // (BC’D).
Đúng 0
Bình luận (0)
Chứng minh các định lí sau:
a) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt còn lại;
b) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó.
a)
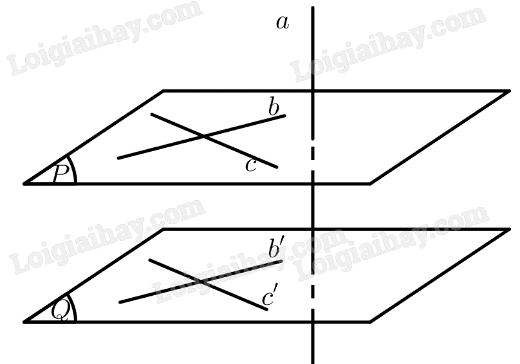
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) song song với nhau và đường thẳng \(a\) vuông góc với \(\left( P \right)\). Ta cần chứng minh \(a \bot \left( Q \right)\).
Trên \(\left( P \right)\) lấy hai đường thẳng \(b,c\) cắt nhau, trên \(\left( Q \right)\) lấy hai đường thẳng \(b',c'\) sao cho \(b'\parallel b,c'\parallel c\).
Vì \(b,c\) cắt nhau nên \(b',c'\) cắt nhau.
\(\begin{array}{l}\left. \begin{array}{l}a \bot \left( P \right) \Rightarrow a \bot b,a \bot c\\b\parallel b',c\parallel c'\end{array} \right\} \Rightarrow a \bot b',a \bot c'\\ \Rightarrow a \bot \left( Q \right)\end{array}\)
Đúng 0
Bình luận (0)
b)
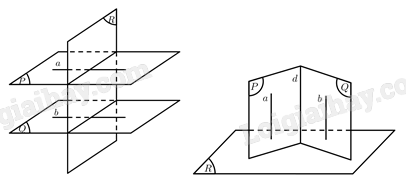
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Ta cần chứng minh \(\left( P \right)\parallel \left( Q \right)\) hoặc \(d \bot \left( R \right)\) với \(d = \left( P \right) \cap \left( Q \right)\).
Vì \(\left( P \right) \bot \left( R \right)\) nên tồn tại đường thẳng \(a \subset \left( P \right)\) sao cho \(a \bot \left( R \right)\), \(\left( Q \right) \bot \left( R \right)\) nên tồn tại đường thẳng \(b \subset \left( Q \right)\) sao cho \(b \bot \left( R \right)\)
\( \Rightarrow a\parallel b\)
Vậy \(\left( P \right)\parallel \left( Q \right)\) hoặc nếu \(\left( P \right),\left( Q \right)\) cắt nhau theo giao tuyến \(d\) thì \(d\parallel a \Rightarrow d \bot \left( R \right)\).
Đúng 0
Bình luận (0)
Chứng minh rằng phép vị tự biến mỗi đường thẳng thành một đường thẳng song song hoặc trùng với nó, biến mỗi mặt phẳng thành một mặt phẳng song song hoặc trùng với mặt phẳng đó.
Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn nửa đường thẳng Ax, By, Cz, Dt ở cùng phía đối với mặt phẳng (ABCD), song song với nhau và không nằm trong mặt phẳng (ABCD). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz và Dt tại A’, B’, C’ và D’.a) Chứng minh: mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt)b) Gọi I AC ∩ BD, J A’C’ ∩ B’D’. Chứng minh: IJ song song với AA’.c) Cho AA’ a, BB’ b, CC’ c. Hãy tính DD’.
Đọc tiếp
Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn nửa đường thẳng Ax, By, Cz, Dt ở cùng phía đối với mặt phẳng (ABCD), song song với nhau và không nằm trong mặt phẳng (ABCD). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz và Dt tại A’, B’, C’ và D’.
a) Chứng minh: mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt)
b) Gọi I = AC ∩ BD, J = A’C’ ∩ B’D’. Chứng minh: IJ song song với AA’.
c) Cho AA’ = a, BB’ = b, CC’ = c. Hãy tính DD’.
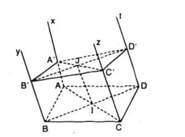
a) Do ABCD là hình bình hành, nên AB // DC
=> AB // (Cz, Dt) (1)
Theo giả thiết Ax // Dt nên Ax // (Cz, Dt) (2)
Từ (1) và (2) suy ra: (Ax, By) // (Cz, Dt)
b) Mặt phẳng β cắt 2 mặt phẳng song song ( Ax, By), (Cz, Dt) theo hai giao tuyến là A’B’và C’D’ nên A’B’// C’D’. (3)
Chứng minh tương tự (Ax, Dt) song song với (By,Cz).Và mặt phẳng β cắt 2 mặt phẳng song song (Ax, Dt), (By, Cz) theo hai giao tuyến là A’D’và B’C’ nên A’D’// B’C’ (4)
Từ (3) và (4) suy ra: tứ giác A’B’C’D’ là hình bình hành.
=> J là trung điểm của A’C’ ( tính chất hình bình hành).
Tứ giác AA’C’C là hình thang vì có: AA’ // CC’ ( giả thiết). Lại có, I và J lần lượt là trung điểm của AC và A’C’ nên IJ là đường trung bình của hình thang
=> IJ// AA’// CC’ ( đpcm).
c) Vì IJ là đường trung bình của hình thang ACC’A’ nên IJ = 1/2(AA’ + CC’)
IJ cũng là đường trung bình của hình thang BDD’B’: IJ = 1/2(BB’ + DD’)
Từ đây suy ra: DD’ + BB’ = AA’ + CC’
=> DD’ = AA’ + CC’ – BB’ = a + c – b
Đúng 0
Bình luận (0)














