Diện tích hình vuông có bốn đỉnh nằm trên hai đường thẳng song song d 1 : 2 x − 4 y + 1 = 0 v à d 2 : − x + 2 y + 10 = 0 là:
A.1/20
B.121/20
C.81/20
D.441/20
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số y = log a x , y = log a x , y = log a 3 x , với (x>0;a>1). Giá trị của a là
A. a = 6 3
B. a = 6 6
C. a = 3
D. a = 3 6
Các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số y = log a x , y = log a x y = log a 3 x với (x>0;a>1)
⇒ Giả sử A ( x 1 ; log a x 1 ) ; B ( x 2 ; 2 log a x 2 ) ; C ( x 3 ; 3 log a x 3 )
Do AB//Ox nên log a x 1 = log a x 2 ⇔ x 1 = x 2 2
Khi đó:
A ( x 2 2 ; log a x 2 ) ; B ( x 2 ; 2 log a x 2 ) ; ⇒ A B = x 2 2 - x 2
Hình vuông ABCD có diện tích bằng 36
![]()


⇔ x 2 = 3 ⇒ x 1 = 9
![]()
![]()
Mặt khác, do AB // Ox nên BC // Oy ⇒ x 3 = 3
![]()
C ( 3 ; log a x 3 )
![]()
![]()
![]()
Chọn đáp án D.
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có diện tích là 36, đường thẳng chứa cạnh AB song song với Ox, các đỉnh A, B, C lần lượt nằm trên các đồ thị hàm số y = loga x, y = log a x , y = log a 3 x với a là số thực lớn hơn 1. Tìm a.
![]()
![]()
![]()
![]()
Đáp án D.
Do AB//Ox => A, B nằm trên đường thẳng y = m ( m ≠ 0 )
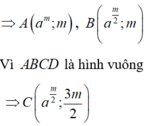
Do SABCD = 36
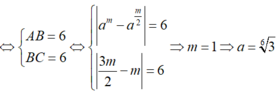 .
.
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số
y = log a x , y = log a x , y = log a 3 x , với x > 0 , a > 1 .
Giá trị của a là:
A. a = 6 3
B. a = 6 6
C. a = 3
D. a = 3 6
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số y = log a x , y = log a x , y = log a 3 x , với x > 0 , a > 1 . Giá trị của a là:
A. a = 6 3
B. a = 6 6
C. a = 3
D. a = 3 6
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có diện tích là 36, đường thẳng chứa cạnh AB song song với Ox, các đỉnh A, B, C lần lượt nằm trên các đồ thị hàm số y = log a x , y = log a x , y = log a 3 x với a là số thực lớn hơn 1. Tìm a.
A. a = 3
B. a = 6 3
C. a = 6
D. a = 3 6
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có diện tích là 36, đường thẳng chứa cạnh AB song song với Ox, các đỉnh A, B, C lần lượt nằm trên các đồ thị hàm số y = log a x , y = log a x , y = log a 3 x với a là số thực lớn hơn 1. Tìm a
A. a = 3
B. a = 6 3
C. a = 6
D. a = 3 6
Cho hình chữ nhật ABCD. Qua một điểm M tùy ý nằm ở bên trong hình chữ nhật đó, kẻ các đường thẳng song song với các hình chữ nhật, chia hình chữ nhật thành 4 hình chữ nhật nhỏ. CMR ít nhất một trong hai hình chữ nhật nhỏ chứa đỉnh A hoặc đỉnh C có diện tích không vượt quá 1/4 diện tích hình chữ nhật ABCD
Cho bốn mệnh đề sau:
(1) Nếu hai mặt phẳng α v à β song song với nhau thì mọi đường thẳng nằm trong mặt phẳng α đều song song với β .
(2) Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau.
(3) Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.
(4) Có thể tìm được hai đường thẳng song song mà mỗi đường thẳng cắt đồng thời hai đường thẳng chéo nhau cho trước
Trong các mệnh đề trên có bao nhiêu mệnh đề sai?
A. 4
B. 2
C. 3
D. 1
Đáp án C
Mệnh đề 1 đúng.
Mệnh đề 2 sai vì 2 đường thẳng đó có thể chéo nhau.
Mệnh đề 3 sai vì 2 đường thẳng đó có thể song song.
Mệnh đề 4 sai