Đáp án D.
Do AB//Ox => A, B nằm trên đường thẳng y = m ( m ≠ 0 )
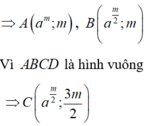
Do SABCD = 36
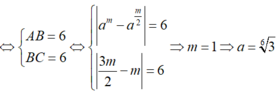 .
.
Đáp án D.
Do AB//Ox => A, B nằm trên đường thẳng y = m ( m ≠ 0 )
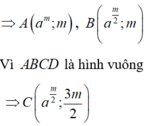
Do SABCD = 36
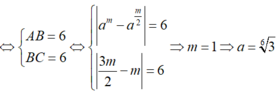 .
.
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có diện tích là 36, đường thẳng chứa cạnh AB song song với Ox, các đỉnh A, B, C lần lượt nằm trên các đồ thị hàm số y = log a x , y = log a x , y = log a 3 x với a là số thực lớn hơn 1. Tìm a
A. a = 3
B. a = 6 3
C. a = 6
D. a = 3 6
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số
y = log a x , y = log a x , y = log a 3 x , với x > 0 , a > 1 .
Giá trị của a là:
A. a = 6 3
B. a = 6 6
C. a = 3
D. a = 3 6
Trong mặt phẳng tọa độ Oxy, cho đồ thị hàm số y = x + 1 x - 1 . A và B là hai điểm thay đổi trên đồ thị sao cho tiếp tuyến của đồ thị tại A và B song song với nhau. Biết rằng đường thẳng AB luôn đi qua một điểm cố định. Tọa độ của điểm đó là
![]()
![]()
![]()
![]()
Cho hình vuông ABCD có diện tích bằng 36, A B → là một vectơ chỉ phương của đường thẳng y=0, các điểm A, B, C lần lượt nằm trên đồ thị hàm số y = log a x , y = 2 log a x , y = 3 log a x . Tìm a.
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ, cho hình chữ nhật (H) có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là A (-1; 0) và C ( m ; m ) , với m > 0. Biết rằng đồ thị hàm số y= x chia hình (H) thành hai phần có diện tích bằng nhau, tìm m .
![]()
![]()
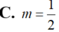
![]()
Trong mặt phẳng tọa độ, cho hình chữ nhật (H) có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là A(-1;0) và C ( m ; m ) , với m>0. Biết rằng đồ thị hàm số y = x chia hình (H) thành hai phần có diện tích bằng nhau, tìm m
![]()
![]()
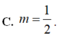
![]()
Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường tròn C 1 và C 2 lần lượt có phương trình x - 1 2 + y - 2 2 = 1 và x + 1 2 + y 2 = 1 . Biết đồ thị hàm số y = a x + b x + c đi qua tâm của C 1 , đi qua tâm của C 2 và có các đường tiệm cận tiếp xúc với cả C 1 và C 2 . Tổng a+b+c là
A. 8
B. 2
C. -1
D. 5
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng ∆ : x + y - 5 = 0 và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương.
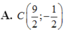
![]()
![]()
![]()
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 2 x 2 + 1 trục Ox và đường thẳng x=1 bằng a b - ln 1 + b c với a,b,c là các nguyên số dương. Khi đó giá trị của a+b+c là:
A. 11.
B. 12.
C. 13.
D. 14.