Giải phương trình sau đây : 2 i - 1 i + 2 z = 3 i + 1 i - 3
A. z = 2.
B. z = -1.
C. z = -i.
D. z = 2i.
Giải các phương trình sau đây (2 + i)z = z + 2i - 1
A. z = 1 + i.
B. z = 0,5 + 1,5i.
C. z = 2+ i.
D. Đáp án khác.
Giải các phương trình sau trên tập số phức: 3x(2 – i) + 1 = 2ix(1 + i) + 3i
Giải các phương trình sau: (1+3i)z-(2+5i)=(2+i)z
(1 + 3i)z - (2 + 5i) = (2 + i)z
⇔ (1 + 3i).z – (2 + i).z = 2 + 5i
⇔ [(1 + 3i) – (2 + i)].z = 2 + 5i
⇔ (-1 + 2i).z = 2 + 5i

Bài I : Giải các phương trình sau
1) 3x – 2( x – 3 ) = 6 2)
3) ( x – 1 )2 = 9 ( x + 1 )2 4)
1) \(3x-2x+6=6\Leftrightarrow x=0\)
2) \(4\left(2x-1\right)-12x-12=3\left(x+2\right)\)
\(\Leftrightarrow8x-4-12x-12-3x-6=0\)
\(\Leftrightarrow7x=-22\Leftrightarrow x=\dfrac{-22}{7}\)
3, \(\left(x-1\right)2=9\left(x+1\right)2\)
\(\Leftrightarrow2x-2\) \(=18x+18\)
\(\Leftrightarrow2x-18x=18+2\)
\(\Leftrightarrow-16x\) \(=20\)
\(\Leftrightarrow x\) \(=\dfrac{-5}{4}\)
Vậy pt đã cho có tập nghiệm là S= \(\left\{\dfrac{-5}{4}\right\}\)
4, \(\dfrac{x-4}{x-1}+\dfrac{x+4}{x+1}=2\) ( ĐKXĐ : \(x\ne\pm1\) )
\(\Leftrightarrow\dfrac{\left(x-4\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{\left(x+4\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{2\left(x+1\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow x^2-3x-4+x^2+3x-4=2x^2-2\)
\(\Leftrightarrow2x^2-8-2x^2+2=0\)
\(\Leftrightarrow0\) \(=6\) ( Vô lí )
Vậy pt đã cho vô nghiệm
Giải phương trình sau trên tập số phức:
(1 – i)z + (2 – i) = 4 – 5i
(Đề thi tốt nghiệp THPT năm 2011)
(1 − i)z + (2 − i) = 4 − 5i
⇔ (1 − i)z = 4 − 5i – 2 + i
⇔(1 − i)z = 2 − 4i
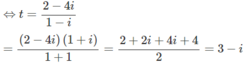
Giải phương trình sau trên tập số phức: (1 – i)z + (2 – i) = 4 – 5i (Đề thi tốt nghiệp THPT năm 2011)
(1 − i)z + (2 − i) = 4 − 5i
⇔ (1 − i)z = 4 − 5i – 2 + i
⇔(1 − i)z = 2 − 4i
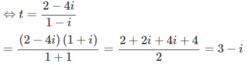
Giải các phương trình sau trên tập số phức:
a) (3 + 4i)x = (1 + 2i)(4 + i)
b) 2ix + 3 = 5x + 4i
c) 3x(2 – i) + 1 = 2ix(1 + i) + 3i
a) (3 + 4i)x = (1 + 2i)(4 + i)
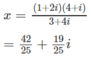
b) 2ix + 3 = 5x + 4i
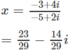
c) 3x(2 – i) + 1 =2ix(1 + i) + 3i
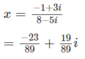
Toán thi vào lớp 10 đây
Bài 1:
Giải các phương trình và hệ phương trình sau:
a) x2 - 8x + 15 = 0.
b) 2x2 - √2x - 2 = 0.
c) x4 - 5x2 - 6 = 0.
![]()
Giải các phương trình và hệ phương trình sau:
a) x2 - 8x + 15 = 0.
Δ' = 42 - 15 = 1
↔ x = 4 + 1 = 5 hay x = 4 - 1 = 3
b) 2x2 - √2x - 2 = 0. (2)
Δ = 2 - 4(2)(-2) = 18
(2) ↔ x = (√2 + 3√2)/4 = √2 hay x = (√2 - 3√2)/4 = -√2/2
c) x4 - 5x2 - 6 = 0
Đặt u = x2 ≥ 0 pt thành:
u2 - 5u - 6 = 0 ↔ u = -1 (loại) hay u = 6
Do đó pt ↔ x2 = 6 ↔ x = ±√6.

Giải các phương trình sau : 2 4x – 2 a) 2x - 3 = 5 b) (x + 2)(3x - 15) 0 z +1 I - 2 (x+ 1) (2 – 2) Câu 2: (2 điểm) số a) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục 2x + 2 <2+ 3 b) Tìm x để giá trị của biểu thức 3x - 4 nhỏ hơn giá trị của biểu thức 5x - 6
1:
a: 2x-3=5
=>2x=8
=>x=4
b: (x+2)(3x-15)=0
=>(x-5)(x+2)=0
=>x=5 hoặc x=-2
2:
b: 3x-4<5x-6
=>-2x<-2
=>x>1
Số phức z nào dưới đây là nghiệm phương trình (1+i) z 2 - ( 2 - i ) z ¯ + i - 2 = 0 ?
A. z = 4
B. z = 1 + i
C. z = -2i
D. z = 2 - i