Cho H là trung điểm của đoạn thẳng EF. Biết HE = 15cm.
Những câu hỏi liên quan
Vẽ ba điểm H và F sao cho E nằm giữa H và F. Gọi M là trung điểm của đoạn thẳng EF. Tính độ dài đoạn thẳng EF và HF biết Me =3cm và HE = 4 cm
Vẽ ba điểm H và F sao cho E nằm giữa H và F. Gọi M là trung điểm của đoạn thẳng EF. Tính độ dài đoạn thẳng EF và HF biết ME=3cm và HE = 4 cm
ME=MF=3cm
=>EF=2*3=6cm
HF=HE+EF=6+4+10cm
Đúng 0
Bình luận (0)
Vẽ ba điểm H và F sao cho E nằm giữa H và F. Gọi M là trung điểm của đoạn thẳng EF. Tính độ dài đoạn thẳng EF và HF biết ME =3cm và HE = 4 cm
cho đoạn thẳng EF,H là một điểm thuộc đoạn thẳng EF,K là trung điểm của EF biết EH =5cm HF=7cm tính độ dài đoạn thẳng HK
EF=EH+HF=5+7=12CM
VÌ K LÀ TRUNG ĐIỂM EF NÊN EK=EF:2=12:2=6CM
HK=EF-EH=6-5=1CM
cho đoạn thẳng DE = 15cm gọi F là điểm nằm giữa DE sao cho 2DF = 3DE tính DF và DE
cho đoạn thẳng DE = 15cm gọi F là điểm nằm giữa DE sao cho DF-EF =3cm tính DF và EF
cho đoạn thẳng CD lấy m là trung điểm của CD biết CM= 15cm .Tính CD
Lời giải:
$M$ là trung điểm của $CD$ nên $CM=\frac{1}{2}CD$
$\Rightarrow 15=\frac{1}{2}CD$
$\Rightarrow CD=30$ (cm)
Đúng 0
Bình luận (0)
Vì M là trung điểm của CD nên CM = MD = 15 (cm)
Do đó CD = CM + MD = 15 + 15 = 30 (cm)
Đúng 0
Bình luận (0)
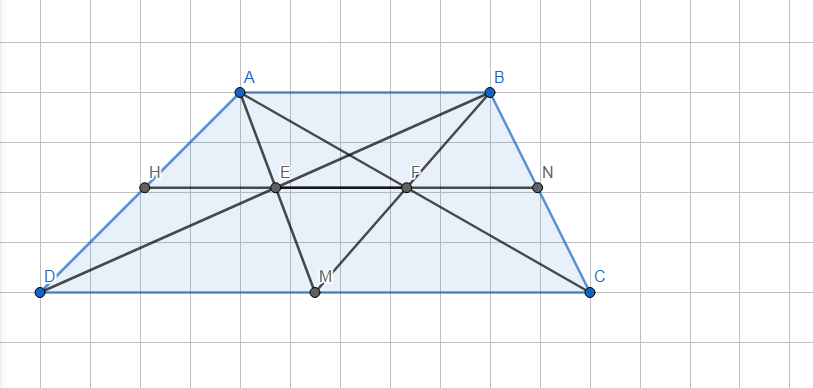
Cho hình thang ABCD có hai đáy là AB và CD. Gọi M là trung điểm của CD, E là giao điểm của MA và BD, F là giao điểm của MB và AC.
a) Chứng minh EF // AB
b) Đường thẳng EF cắt AD, BC lần lượt tại H và N. Chứng minh HE = EF = FN.
c) Biết AB = 7,5 cm, CD = 12 cm. Tính độ dài HN.
- Hình vẽ:
a) - Xét △EDM có:
AB//DM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) (định lí Ta-let) (1).
- Xét △FCM có:
AB//CM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{BF}{MF}=\dfrac{AB}{CM}\) (định lí Ta-let) (2).
- Từ (1) và (2) và \(CM=DM\) (M là trung điểm BC) suy ra:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\).
- Xét △ABM có:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\) (cmt)
=>\(EF\)//\(AB\) (định lí Ta-let đảo)nên\(EF\)//\(AB\)//\(CD\)
b) -Xét △ADM có:
HE//DM (cmt).
=>\(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (định lí Ta-let). (3)
- Xét △ACM có:
EF//CM (cmt)
=>\(\dfrac{EF}{CM}=\dfrac{AE}{AM}\) (định lí Ta-let) (4)
- Từ (3) và (4) và \(DM=CM\) (M là trung điểm BC) suy ra: \(HE=EF\)
-Xét △BDM có:
EF//DM (cmt).
=>\(\dfrac{EF}{DM}=\dfrac{BF}{BM}\)(định lí Ta-let). (5)
- Xét △BCM có:
NF//CM (cmt)
=>\(\dfrac{NF}{CM}=\dfrac{BF}{BM}\) (định lí Ta-let) (6)
- Từ (5) và (6) và \(CM=DM\) (M là trung điểm BC) suy ra: \(NF=EF\)
Mà \(HE=EF\) nên \(HE=EF=NF=\dfrac{1}{3}HN\).
c) -Ta có: \(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (cmt)
=>\(\dfrac{DM}{HE}=\dfrac{AM}{AE}\).
=>\(\dfrac{DM}{HE}-1=\dfrac{EM}{AE}\) (7)
- Ta có: \(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) nên \(\dfrac{EM}{AE}=\dfrac{DM}{AB}\). (8)
- Từ (7) và (8) suy ra:
\(\dfrac{DM}{HE}-1=\dfrac{DM}{AB}\)
=>\(\dfrac{DM}{HE}=\dfrac{DM}{AB}+1=\dfrac{DM+AB}{AB}\)
=>\(HE=\dfrac{AB.DM}{AB+DM}=\dfrac{7,5.\left(12.\dfrac{1}{2}\right)}{7,5+\left(12.\dfrac{1}{2}\right)}=\dfrac{10}{3}\)
=>\(HN=3HE=3.\dfrac{10}{3}=10\) (cm).
Đúng 1
Bình luận (0)
Cho đoạn thẳng EF=8cm.M là trung điểm của đoạn thẳng EF. I là trung điểm của đoạn thẳng ME,K là trung điểm của đoạn thẳng MF. tìm độ dài IK và EK
Cho 3 điểm thẳng hàng A, B, C. Biết M là trung điểm của AB, P là trung điểm của BC. Tính độ dài đoạn MP biết AB = 15cm và BC = 9cm.
Vì M là trung điểm của đoạn thẳng AB nên ta có:(1)
MB = AB/2 = 15:2 = 7,5 (cm)
Vì P là trung điểm của đoạn thẳng nên ta có:(2)BP = BC/2 = 9:2 = 4,5 (cm)
Từ (1) và (2), ta có độ dài của đoạn thẳng MP là:MP = MB+BP = 7,5+4,5 = 12 (cm)
Đ/s: 12 cm
Đúng 0
Bình luận (0)