Không giải hệ phương trình, dự đoán số nghiệm của hệ
A. 0
B. Vô số
C. 1
D. 2
Không giải hệ phương trình, dự đoán số nghiệm của hệ − x + 5 y = − 1 5 x + y = 2
A. Vô số nghiệm
B. Vô nghiệm
C. Có nghiệm duy nhất
D. Có hai nghiệm phân biệt
Xét hệ phương trình − x + 5 y = − 1 5 x + y = 2 có − 1 5 ≠ 5 1 nên hệ phương trình có nghiệm duy nhất
Đáp án: C
Không giải hệ phương trình, dự đoán số nghiệm của hệ − 2 x + y = − 3 3 x − 2 y = 7
A. Vô số nghiệm
B. Vô nghiệm
C. Có nghiệm duy nhất
D. Có hai nghiệm phân biệt
Xét hệ phương trình − 2 x + y = − 3 3 x − 2 y = 7 có − 2 3 ≠ 1 − 2 nên hệ phương trình có nghiệm duy nhất
Đáp án: C
Không giải hệ phương trình, dự đoán số nghiệm của hệ 2 x − 2 y = 3 3 2 x − 6 y = 5
A. Vô số nghiệm
B. Vô nghiệm
C. Có nghiệm duy nhất
D. Có hai nghiệm phân biệt
Xét hệ phương trình 2 x − 2 y = 3 3 2 x − 6 y = 5 có 2 3 2 = − 2 − 6 ≠ 3 5 ⇔ 1 3 = 1 3 ≠ 3 5 nên hệ phương trình vô nghiệm
Đáp án: B
Không giải hệ phương trình, dự đoán số nghiệm của hệ - 2 x + y = - 3 3 x - 2 y = 7
A. 0
B. Vô số
C. 1
D. 2
Đáp án C
Tập nghiệm phương trình -2x + y = -3 được biểu diễn bởi đường thẳng -2x + y = -3
Tập nghiệm phương trình 3x – 2y = 7 được biểu diễn bởi đường thẳng 3x – 2y = 7
Ta có 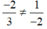 ⇒ phương trình có một nghiệm duy nhất
⇒ phương trình có một nghiệm duy nhất
Xét hpt \(\hept{\begin{cases}2x+y=3\left(a=2;b=1;c=3\right)\\3x-y=1\left(a'=3;b'=-1;c'=1\right)\end{cases}}\)
Ta có \(\frac{a}{a'}=\frac{2}{3}\)và \(\frac{b}{b'}=\frac{1}{-1}=-1\), do đó \(\frac{a}{a'}\ne\frac{b}{b'}\), dẫn đến hpt đã cho chỉ có 1 nghiệm duy nhất.
\(\Rightarrow\)Chọn A
cho hệ phương trình \(\left\{{}\begin{matrix}4x-my-m-6=0\\mx-y-2m=0\end{matrix}\right.\)
tìm m để : a. hệ phương trình vô nghiệm
b. hệ phương trình có nghiệm duy nhất
c. hệ phương trình có vô số nghiệm
Câu 1: Nêu sự tương giao giữa hai đường thẳng (D): ax+by=c và (D'): a'x+b'y=c' với số nghiệm của hệ phương trình \(\begin{cases} ax+by=c\\ a'x+b'y=c' \end{cases} \)
Câu 2: Không giải hệ phương trình, hãy cho biết số nghiệm của các hệ phương trình sau:
a) \(\begin{cases} y=-2x-5\\ -4x-2y=10 \end{cases} \) b) \(\begin{cases} 2x-y=1\\ 3x+y=3 \end{cases} \)
Câu 3: pt bậc hai một ẩn là gì ? Cho vd ?
Câu 4: Nêu tính chất của hàm số y=ax2 (a \(\ne\) 0). Áp dụng vào hàm số y = \(\dfrac{1}{2}\)x2 ; y = -3x2.
Câu 5: Điểm A ( -2 ; -1 ) có thuộc đồ thị hàm số y = \(\dfrac{-x^2}{4}\) không ? Vì sao ?
Câu 6: Điểm nào sau đây thuộc đồ thị hàm số y = \(\dfrac{-x^2}{2}\) :
a) A ( -2 ; 2 ) b) B ( 4 ; -8 ) c) C ( 2 ; 2 )
6:
a: f(-2)=-1/2*(-2)^2=-2
=>Loại
b: f(4)=-1/2*4^2=-8=yB
=>B thuộc (P)
c: f(2)=-1/2*2^2=-2
=>Loại
5: f(-2)=-1/4*(-2)^2=-1/4*4=-1
=>A thuộc (P)
4: tính chất:
Nếu a>0 thì hàm số đồng biến khi x>0 và nghịch biến khi x<0
Nếu a<0 thì hàm số đồng biến khi x<0 và nghịch biến khi x>0
y=1/2x^2: Hàm số đồng biến khi x>0 và nghịch biến khi x<0
y=-3x^2: Hàm số đồng biến khi x<0 và nghịch biến khi x>0
Khi giải một hệ phương trình bậc nhất hai ẩn, ta biến đổi hệ phương trình đó để được một hệ phương trình mới tương đương , trong đó có một phương trình một ẩn. Có thể nói gì về số nghiệm của hệ đã cho nếu phương trình một ẩn đó:
a) Vô nghiệm? ; b) Có vô số nghiệm?
a) Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.
b) Hệ đã cho có vô số nghiệm.
Cho hệ phương trình x + my =2m hoặc mx + y = 1-m (m là tham số )
1.Tìm các giá trị của m để hệ phương trình :
a)Có nghiệm duy nhất. Tìm nghiệm duy nhất đó
b)Vô nghiệm
c)Vô số nghiệm
2.Trong trường hợp hệ phương trình có nghiệm duy nhất (x,y)
a)Hãy tìm giá trị m nguyên để x và y cùng nguyên
b)tìm hệ thức liên hệ giữa x và y không phụ thuộc m