Một con lắc đơn có chiều dài l = 1 m treo ở trần một thang máy, khi thang máy đi xuống nhanh dần đều với gia tốc a = g 2 (g = π 2 m / s 2 ) thì chu kì dao động bé của con lắc là
A. 4 s
B. 2,83 s
C. 1,64 s
D. 2 s
Một con lắc đơn có chiều dài l = 1 m treo ở trần một thang máy, khi thang máy đi xuống nhanh dần đều với gia tốc a = g 2 (g = π2 m/s2) thì chu kì dao động bé của con lắc là
A. 4 s.
B. 2,83 s.
C. 1,64 s.
D. 2 s.
Một con lắc đơn có chiều dài l treo trong trần một thang máy. Khi thang máy chuyển động nhanh dần đều đi lên với gia tốc có độ lớn a (a < g) thì con lắc dao động với chu kì T1. Khi thang máy chuyển động chậm dần đều đi lên với gia tốc có độ lớn a thì con lắc dao động với chu kì T2 = 2T1. Độ lớn gia tốc a bằng
A. g/5.
B. 2g/3.
C. 3g/5.
D. g/3.
Đáp án C
Phương pháp: Sử dụng lí thuyết về bài toán con lắc đơn chịu tác dụng của lực quán tính
Cách giải:
+ Khi thang máy đi lên NDĐ với gia tốc có độ lớn là a thì gia tốc trọng trường hiệu dụng : g1 = g + a
=> Chu kì dao động: T 1 = 2 π l g + a
+ Khi thang máy đi lên CDĐ với gia tốc có độ lớn là a thì gia tốc trọng trường hiệu dụng : g2 = g – a
=> Chu kì dao động T 2 = 2 π l g - a
+ Theo đề bài T 2 = 2 T 1 ⇒ π l g - a = 2 l g + a => g + a = 4(g-a) => a = 3g/5
=> Chọn C
Con lắc đơn có chiều dài ℓ treo trong trần một thang máy. Khi thang máy chuyển động nhanh dần đi lên với gia tốc có độ lớn a (a < g) thì dao động với chu kỳ T 1 . Khi thang máy chuyển động chậm dần đều đi lên với gia tốc có độ lớn a thì dao động với chu kỳ T 2 = 2 T 1 . Độ lớn gia tốc a bằng
A. g/5.
B. 2g/3.
C. 3g/5.
D. g/3.
Đáp án C
+ Chu kì dao động của con lắc trong hai trường hợp:
T 1 = 2 π l g + a T 2 = 2 T 1 = 2 π l g - a → g + a g - a = 4 → a = 0 , 6 g .
Con lắc đơn có chiều dài ℓ treo trong trần một thang máy. Khi thang máy chuyển động nhanh dần đi lên với gia tốc có độ lớn a (a < g) thì dao động với chu kỳ T1. Khi thang máy chuyển động chậm dần đều đi lên với gia tốc có độ lớn a thì dao động với chu kỳ T2 = 2T1. Độ lớn gia tốc a bằng
A. g/5.
B. 2g/3.
C. 3g/5.
D. g/3.
Chu kì dao động của con lắc trong hai trường hợp:
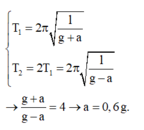
Đáp án C
Một con lắc đơn treo trên trần một thang máy. Khi thang máy đi xuống nhanh dần đều sau đó chậm dần đều với cùng gia tốc thì chu kì dao động điều hòa của con lắc lần lượt là T1 = 2,17 s và T2 = 1,86 s. Lấy g = 9,8 m/s2 . Chu kì dao động của con lắc lúc thang máy đứng yên và gia tốc của thang máy là
Thang máy đi xuống nhanh dần đều thì 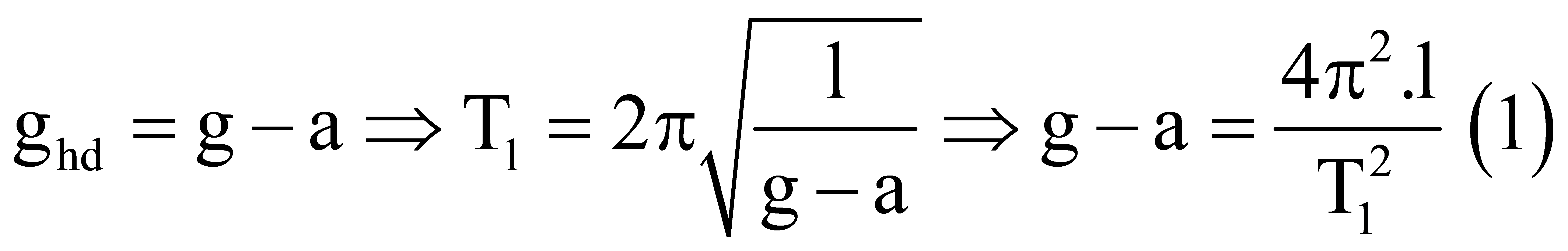 Thang máy đi xuống chậm dần đều thì
Thang máy đi xuống chậm dần đều thì 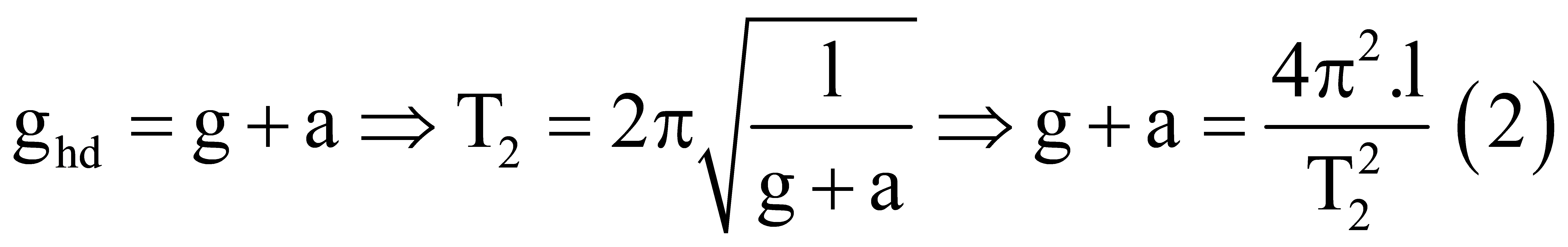 Khi thang máy đứng yên thì
Khi thang máy đứng yên thì 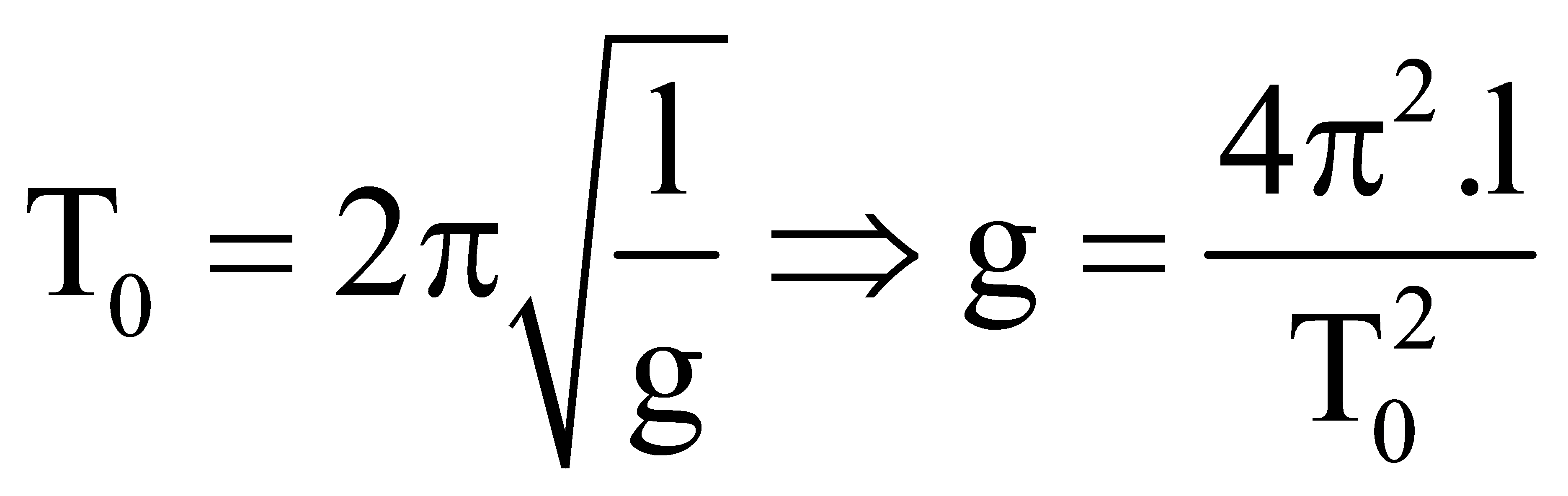 .
.
Từ (1) và (2) 
Thang máy đi xuống nhanh dần đều thì 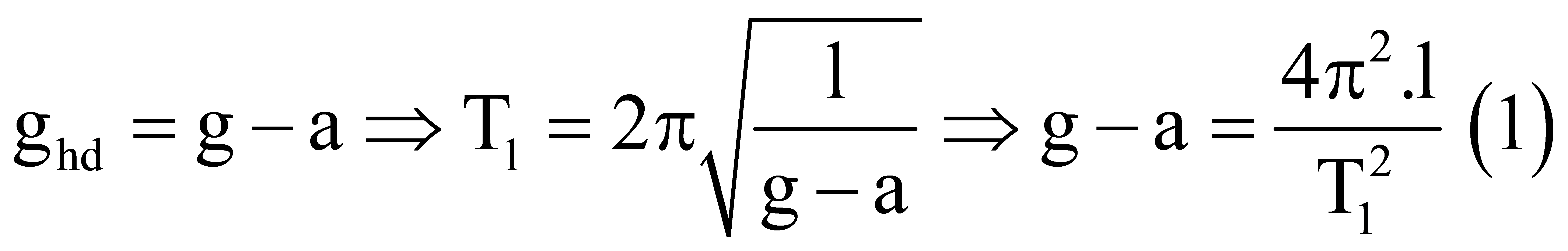 Thang máy đi xuống chậm dần đều thì
Thang máy đi xuống chậm dần đều thì 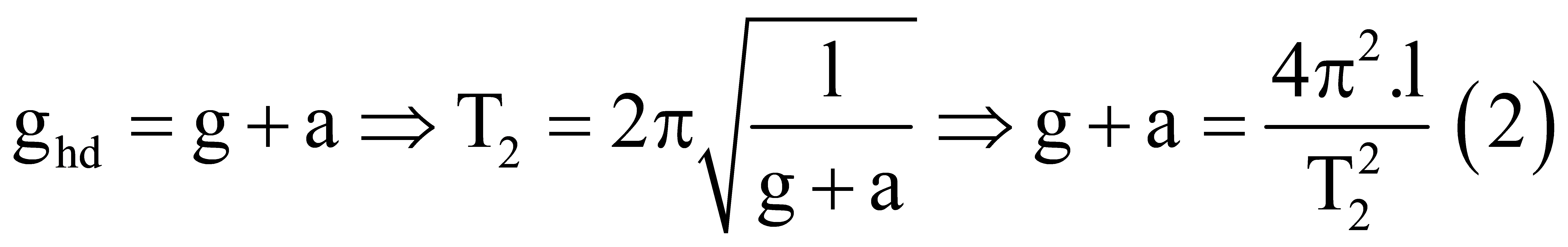 Khi thang máy đứng yên thì
Khi thang máy đứng yên thì 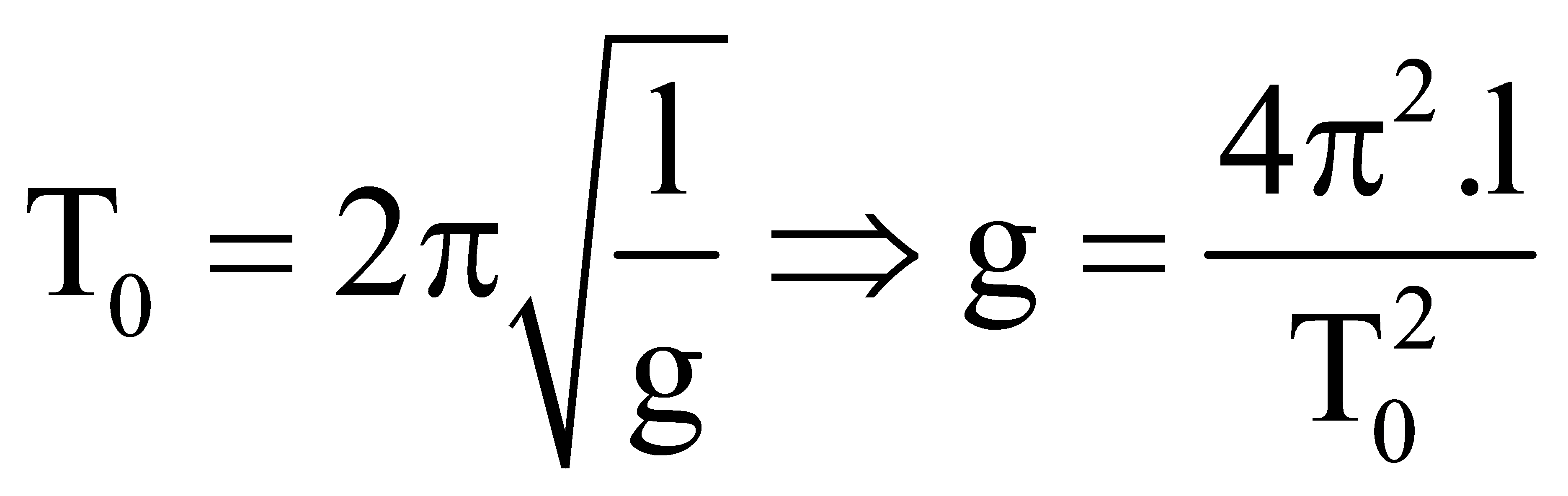 .
.
Từ (1) và (2)  .
.
Biết gia tốc trọng trường là g. Một đồng hồ quả lắc treo trên trần của một chiếc thang máy, khi thang máy đi lên nhanh dần đều với gia tốc a thì chu kì dao động của con lắc đơn là
A. T = 2 π l g - a 2
B. T = 2 π l g + a
C. T = 2 π l g - a
D. T = 2 π l ( g - a ) g 2
Một con lắc đơn được treo ở trần một thang máy. Khi thang máy đứng yên, con lắc dao động với tần số 0,25 Hz. Khi thang máy đi xuống thẳng đứng, chậm dần đều với gia tốc bằng một phần ba gia tốc trọng trường tại nơi đặt thang máy thì con lắc đơn dao động với chu kì bằng
A. 3 s
B. 2 3 s
C. 3 2 s
D. 3 3 s
Trong thang máy, tại trần người ta treo một con lắc lò xo có độ cứng k = 25 N/m, vật nặng có khối lượng 400 g. Khi thang máy đứng yên ta cho con lắc dao động điều hòa, chiều dài con lắc thay đổi từ 32 cm đến 48 cm. Tại th ời điểm mà vật ở vị trí thấp nhất thì cho thang máy đi xuống nhanh dần đều với gia tốc a = g/10. Lấy g = π2 m/s2 = 10 m/s2. Biên độ dao động của vật trong trường hợp này là
A. 19,2 cm.
B. 9,6 cm.
C. 8,5 cm.
D. 17 cm.
Giải thích: Đáp án B
Phương pháp: Sử dụng lí thuyết về con lắc lò xo chịu tác dụng của ngoại lực
Cách giải:
- Khi thang máy chưa chuyển động
+ Tần số góc: 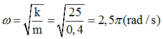
+ Biên độ dao động: 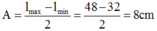
- Khi thang máy chuyển động nhanh dần đều đi xuống thì con lắc chịu thêm tác dụng của lực quán tính
F
q
⇀
hướng lên, có độ lớn ![]()
=> VTCB mới là 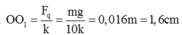
=> Khi đó so với VTCB vật đang ở li độ x1 = A + 1,6 = 9,6cm, vận tốc v1=v=0
=> Biên độ dao động mới là 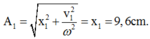
Một con lắc đơn được treo vào trần thang máy tại nơi có g = 10 m/ s 2 . Khi thang máy đứng yên con lắc có chu kì dao động nhỏ là T = 1s và biên độ góc là α 0 = 9 0 . Đúng lúc vật nhỏ ở biên dương thì thang máy đi lên nhanh dần đều với gia tốc 2,5 m/ s 2 . Chu kì và biên độ của con lắc đơn từ thời điểm đó là
A. 0,8944s và 9 0
B. 1,1276s và 7 , 5 0
C. 1538s và 10 , 8 0
D. 0,8756s và 9 0
Đáp án A
Tại vị trí biên, vận tốc của con lắc bằng 0. Việc thang máy đi lên nhanh dần đều không làm thay đổi vị trí cân bằng của con lắc → biên độ dao động không đổi α 0 = 9 0
Chu kì dao động
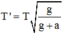
= 0,89s