Cho hình chóp S.ABCD có đáy là hình chữ nhật, A B = a 3 và A D = a . Đường thẳng SA vuông góc với mặt phẳng đáy và S A = a . Thể tích khối cầu ngoại tiếp hình chóp S.BCD bằng
A. 5 π a 3 5 6
B. 5 π a 3 5 24
C. 3 π a 3 5 25
D. 3 π a 3 5 8
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB= a 3 và AD=a. Đường thẳng SA vuông góc với mặt phẳng đáy và SA=a. Thể tích khối cầu ngoại tiếp hình chóp S.BCD bằng
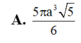
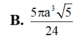
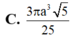
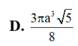
Cho hình chóp S.ABCD có đáy là hình chữ nhật, A B = a 3 , A D = a . Đường thẳng SA vuông góc với đáy và S A = a . Thể tích của khối cầu ngoại tiếp hình chóp S . B C D bằng
A. 5 πa 3 5 6
B. 5 πa 3 5 24
C. 3 πa 3 5 25
D. 3 πa 3 5 8
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB= a 3 và AD = a . Đường thẳng SA vuông góc với mặt phẳng đáy và SA=a. Thể tích khối cầu ngoại tiếp hình chóp S.BCD bằng?
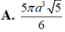
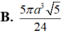
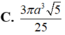
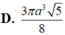
Cho hình chóp S.ABCD có đáy là hình chữ nhật, A B = a 3 và AD = a . Đường thẳng SA vuông góc với mặt phẳng đáy và S A = a . . Thể tích khối cầu ngoại tiếp hình chóp S.BCD bằng?
A. 5 π a 3 5 6
B. 5 π a 3 5 24
C. 3 π a 3 5 25
D. 3 π a 3 5 8
Đáp án A.
Do ABCD là hình chữ nhật nên khối cầu ngoại tiếp hình chóp S.BCD chính là khối cầu ngoại tiếp hình chóp S.ABCD
Khi đó
R = S C 2 = S A 2 + A B 2 + A D 2 2 = a 5 2 ⇒ V = 4 3 π R 3 = 5 π a 3 5 6
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a. Cạnh bên SA vuông góc với đáy và SA=a. Góc giữa đường thẳng SB và CD là
A. 90 o
B. 60 o
C. 30 o
D. 45 o
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a. Cạnh bên SA = a và SA vuông góc với đáy. Tính góc giữa đường thẳng SB và CD
A. 90 ∘
B. 60 ∘
C. 30 ∘
D. 45 ∘
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC= a 3 , SA = a và SA vuông góc với đáy ABCD. Tính sin α , với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).
A. sin α = 7 8
B. sin α = 3 2
C. sin α = 2 4
D. sin α = 3 5
Chọn đáp án C.

ABCD là hình chữ nhật nên BD = 2a, ta có AD//(SBC) nên suy ra
![]()
với AH ⊥ SB. Tam giác SAB vuông cân tại A nên H là trung điểm của SB suy ra A H = a 2 2
Vậy
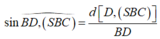
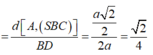
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = a 3 ,SA = a và SA vuông góc với đáy ABCD. Tính sinα, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC)
A . sin α = 7 8
B . sin α = 3 2
C . sin α = 2 4
D . sin α = 3 5
Chọn C
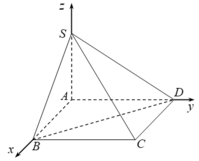
Đặt hệ trục tọa độ Oxyz như hình vẽ. Khi đó, ta có A (0; 0; 0), B (a; 0; 0), D (0; a√3; 0), S (0; 0; a)
Ta có ![]() , nên đường thẳng BD có vectơ chỉ phương là
, nên đường thẳng BD có vectơ chỉ phương là ![]()
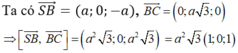
Như vậy, mặt phẳng (SBC) có vectơ pháp tuyến là ![]() . Do đó, α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) thì:
. Do đó, α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) thì:
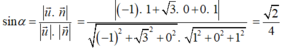
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a,
BC =2a, đường thẳng SA vuông góc với mặt phẳng (ABCD) và
SA =3a . Thể tích của khối chóp S.ABCD bằng
![]()
![]()
![]()
![]()