Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z có phần thực bằng ‒2.
A. Đường thẳng x + 2 = 0
B. Đường thẳng y + 2 = 0
C. Đường thẳng x - 2 = 0
D. Đường thẳng y - 2 = 0
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z có phần thực bằng ‒2.
A. Đường thẳng x + 2 = 0
B. Đường thẳng y + 2 = 0
C. Đường thẳng x - 2 = 0
D. Đường thẳng y - 2 = 0
Đáp án A.
Tập hợp các điểm biểu diễn số phức z có phần thực bằng ‒2 là đường thẳng x + 2 = 0 .
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z có phần thực dương, thỏa mãn z ≤ 2
![]()
![]()

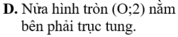
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z có phần thực dương, thỏa mãn z ≤ 2
A. Đường tròn (O;2)
B. Hình tròn (O;2)
C. Nửa hình tròn (O;2) nằm bên trái trục tung
D. Nửa hình tròn (O;2) nằm bên phải trục tung
Trong mặt phẳng tọa độ Oxyz, tập hợp điểm biểu diễn của các số phức z = 2 + b i với b ∈ R là đường thẳng
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxyz, tập hợp điểm biểu diễn của các số phức z=2+bi với bÎR là đường thẳng
A. x = 2
B. Song song với trục Ox
C. y = 2
D. Vuông góc với trục Oy
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
Có bao nhiêu số phức z thỏa mãn z - 2 i = 5 và tập điểm biểu diễn của số phức z trong mặt phẳng tọa độ là đường thẳng ∆ : 3x-y+1=0?
A. 2
B. 1
C. 0
D. Vô số
Chọn A.
Gọi I(0;2) và M z ⇒ M I = 5 suy ra tập điểm biểu diễn của số phức z trong mặt phẳng tọa độ giao điểm của đường tròn (C) tâm I(0;2) bán kính R = 5 và
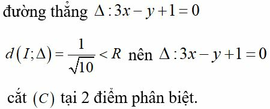
Trong mặt phẳng tọa độ Oxy ,tìm tập hợp biểu diễn các số phức z thỏa mãn điều kiện phần thực bằng 3 lần phần ảo của nó là một
A. Parabol
B. Đường tròn
C. Đường thẳng
D. Elip
\(z=x+i.y\) với \(x=3y\)
\(\Rightarrow x-3y=0\Rightarrow\) tập hợp z là một đường thẳng