Gọi là số cạnh của hình chóp có 101 đỉnh. Tìm n
A. n = 202
B. n = 200
C. n = 101
D. n = 203
Gọi n là số cạnh của hình chóp có 101 đỉnh. Tìm n
A. n = 202
B. 200
C. n = 101
D. 203
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN)
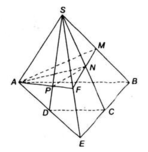
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
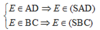
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.
Gọi (T) là hình chóp lục giác đều có cạnh bên bằng 9 cm, cạnh đáy bằng 8 cm và (N) là hình nón có đỉnh là đỉnh của (T) và đáy là đường tròn ngoại tiếp đáy của (T). Thể tích của khối nón (N) (tính bằng c m 3 ) là
![]()
![]()
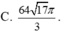
![]()
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC) ?
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN) ?
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN) ?
a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
Cho hình chóp tứ giác đều S.ABCD có Sa=a và S A B ⏜ = 11 π 24 . Gọi Q là trung điểm cạnh SA. Trên các cạnh SB, Sc, SD lần lượt lấy các điểmM, N, P không trùng với các đỉnh hình chóp. Tìm giá trị nhỏ nhất của tổng A M + M N + N P + P Q theo a
A. a 2 4
B. a 3 sin 11 π 12 3
C. a 3 2
D. a 2 sin 11 π 24 3
Đáp án C
Trải khối chóp đều S.ABCD ra mặt phẳng như hình vẽ bên:

Với điểm A=A' và H là trung điểm của AA'
Dễ thấy để A M + M N + N P + P Q nhỏ nhất <=> các điểm A, M, N, P, Q thẳng hàng ⇒ A M + M N + N P + P Q = A Q
Tam giác SAA' có A S A ⏜ = 4 A S B ⏜ = 4 π − 2 11 π 24 = π 3
Mà S A = S A ' ⇒ Δ S A A ' là tam giác đều ⇒ A Q = a 3 2
Cho hình chóp tứ giác đều S.ABCD có SA = a và S A B ⏜ = 11 π 24 . Gọi Q là trung điểm của cạnh SA. Trên các cạnh SB, SC, SD lần lượt lấy các điểm M, N, P không trùng với các đỉnh của hình chóp. Tìm giá trị nhỏ nhất của tổng A M + M N + N P + P Q theo a
A. a 2 sin 11 π 24 3
B. a 3 2
C. a 2 4
D. a 3 sin 11 π 12 3
Chọn đáp án B
Do S.ABCD là hình chóp tứ giác đều nên mỗi mặt bên là một tam giác cân tại đỉnh S.
Theo giả thiết ta có
![]()
Cắt hình chóp theo cạnh bên SA rồi trải các mặt bên thành một mặt phẳng ta được hình vẽ bên sao cho khí ghép lại thì A ≡ A '
Suy ra A S A ' ⏜ = 4 . A S B ⏜ = π 3 và ∆ S A A ' đều cạnh SA = a

Khi đó tổng AM + MN + NP + PQ là tổng của các đường gấp khúc.
Tổng này đạt nhỏ nhất bằng AQ nếu xảy ra trường hợp các điểm A, M, N, P, Q thẳng hàng.
Mà ∆ S A A ' đều có Q là trung điểm SA nên A Q = S A 3 2 = a 3 2
Vậy m i n A M + M N + N P + P Q = a 3 2
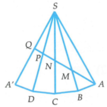
Cho hình chóp tứ giác đều S.ABCD có SA=a và SAB= 11 π 24 . Gọi Q là trung điểm cạnh SA. Trên các cạnh SB,SC,SD lần lượt lấy các điểm M,N,P không trùng với các đỉnh hình chóp. Tìm giá trị nhỏ nhất của tổng AM+MN+NP+PQ theo a
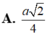
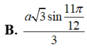
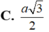
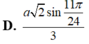
Bt2: cho hình chóp S.ABCD đáy là tứ giác lồi có AB>CD .gọi M,N lần lượt là trung điểm của cạnh SA và SD .a) tìm giao tuyến (SAB) và (SCD).b) tìm giao tuyến của (MNC) và (ABCD).c)tìm giao điểm của MN và (ABN).d) tìm thiết diện của hình chóp vs mp (BMN)
ho hình chóp tứ giác S . A B C D , M là một điểm trên cạnh S C , N là trên cạnh B C . Tìm giao điểm của đường thẳng S D với mặt phẳng ( A M N ) .
Chọn mp(SBD) có chứa SD
Gọi O là giao của AC và BD
K là giao của SO với AN
L giao của BD với AN
\(\left\{{}\begin{matrix}K=SO\cap AN\\SO\subset\left(SBD\right)\\AN\subset\left(AMN\right)\end{matrix}\right.\Leftrightarrow K\in\left(SBD\right)\cap\left(AMN\right)\)
\(\left\{{}\begin{matrix}L=BD\cap AN\\SO\subset\left(SBD\right)\\AN\subset\left(AMN\right)\end{matrix}\right.\Leftrightarrow L\in\left(SBD\right)\cap\left(AMN\right)\)
=>(SBD) giao (AMN)=KL
Gọi P là giao của KL với SD
=>P=SD giao (AMN)