Trên tập số phức, tính tổng môđun bình phương tất cả các nghiệm của phương trình z 4 - 16 = 0 .
![]()
![]()
![]()
![]()
Trên tập số phức, tính tổng môđun bình phương tất cả các nghiệm của phương trình z 4 - 16 = 0
![]()
![]()
![]()
![]()
Tất cả các nghiệm phức của phương trình z 3 − 64 z 2 + 2 = 0 có tổng môđun là
A. 4 + 2 2
B. 4 + 2
C. 8 + 2
D. 12 + 2 2
Tất cả các nghiệm phức của phương trình z 3 - 64 z 2 + 2 = 0 có tổng môđun là
A. 4+2 2 .
B. 4 + 2 .
C. 8 + 2 .
D. 12+2 2
Tất cả các nghiệm phức của phương trình ( z 3 − 64 ) ( z 2 + 2 ) = 0 có tổng môđun là
A. 4 + 2 2
B. 4 + 2
C. 8 + 2
D. 12 + 2 2
Cho số phức z có tập hợp điểm biểu diễn trên mặt phẳng phức là đường tròn có phương trình x 2 + y 2 - 25 = 0 . Tính môđun của số phức z?
![]()
![]()
![]()
![]()
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
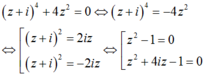
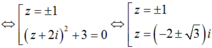
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: 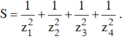
A. 2/5
B. 3/5
C. 5/4
D. 6/7
Chọn C.
Không mất tính tổng quát ta gọi 4 nghiệm của phương trình là:
z1= 1; z2= - 2; z3= 1+ i và z4 = 1 - i
Thay vào biểu thức
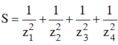
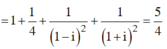
Cho m là số thực, biết phương trình z 2 + m z + 5 = 0 có hai nghiệm phức. Tính tổng môđun của hai nghiệm.
A. 3
B. 5
C. 2 5
D. 4
Tổng môđun các nghiệm phức của phương trình z 2 + 4 z + 5 = 0 bằng
A. 5
B. 3
C. 2 5
D. 2 3