Phương trình z 2 + 3 z + 9 = 0 có hai nghiệm phức z 1 , z 2 . Tính S = z 1 . z 2 + z 1 + z 2
![]()
![]()
![]()
![]()
Đường thẳng ∆ là giao của hai mặt phẳng x + z - 5 = 0 và x - 2 y + - z + 3 = 0 thì có phương trình là:
A. x + 2 1 = y + 1 3 = z - 1
B. x + 2 1 = y + 1 2 = z - 1
C. x - 2 1 = y - 1 1 = z - 3 - 1
D. x - 2 1 = y - 1 2 = z - 3 - 1
Mặt phẳng x + z - 5 = 0 và x - 2 y + - z + 3 = 0 có VTPT lần lượt là
![]()
Đường thẳng ∆ là giao của hai mặt phẳng x + z - 5 = 0 và x - 2 y + - z + 3 = 0 có 1 VTCP là:
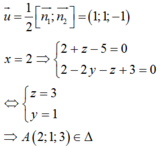
Phương trình đường thẳng ∆ là: .
Chọn C.
trên tập hợp số phức, xét phương trình \(z^2\)-2(2m-1)z+\(m^2\)=0. Có bao nhiêu giá trị của m để phương trình có hai nghiệm phân biệt z1,z2 thỏa mãn \(z1^2\)+\(z2^2\)=2
\(z^2-2\left(2m-1\right)z+m^2=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}z_1+z_2=-\dfrac{b}{a}=2\left(2m-1\right)=4m-2\\z_1z_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)
Ta có :
\(z^2_1+z_2^2=2\)
\(\Leftrightarrow\left(z_1+z_2\right)^2-2z_1z_2=2\)
\(\Leftrightarrow\left(4m-2\right)^2-2m^2-2=0\)
\(\Leftrightarrow16m^2-16m+4-2m^2-2=0\)
\(\Leftrightarrow14m^2-16m+2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m=\dfrac{1}{7}\end{matrix}\right.\)
Ta có phương trình bậc hai trên tập số phức:
z^2 - 2(2m-1)z + m^2 = 0
Theo định lý giá trị trung bình, nếu z1 và z2 là nghiệm của phương trình trên, thì ta có:
z1 + z2 = 2(2m-1) và z1z2 = m^2
Từ phương trình z1^2 + z2^2 = 2, ta suy ra:
(z1+z2)^2 - 2z1z2 = 4
Thay z1+z2 và z1z2 bằng các giá trị đã biết vào, ta được:
(2(2m-1))^2 - 2m^2 = 4
Đơn giản hóa biểu thức ta có:
m^2 - 4m + 1 = 0
Suy ra:
m = 2 + √3 hoặc m = 2 - √3
Vậy, để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, ta cần phải có m = 2 + √3 hoặc m = 2 - √3.
Kết luận: Có hai giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, đó là m = 2 + √3 hoặc m = 2 - √3.
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x+2y+3z-5=0. Đường thẳng Δ vuông góc với (P) cắt d1 và d2 có phương trình là:
![]()
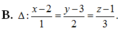
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x + 2 y + 3 z - 5 = 0 . Đường thẳng Δ vuông góc với (P) cắt d 1 và d 2 có phương trình là:
A. ∆ : x - 1 1 = y + 1 2 = z 3
B. ∆ : x - 2 1 = y - 3 2 = z - 1 3
C. ∆ : x - 3 1 = y - 3 2 = z + 2 3
C. ∆ : x - 1 3 = y + 1 2 = z 1
Mặt phẳng đi qua điểm A(1;1;1) và vuông
góc với hai mặt phẳng x + y - z -2 = 0,
x + y + z - 1 = 0 có phương trình là
![]()
![]()
![]()
![]()
Đường thẳng d song song với hai mặt phẳng
(P): 3x + 12y - 3z - 5 = 0,
(Q): 3x - 4y + 9z = 0 và đồng thời cắt
cả hai đường thẳng d 1 : x + 5 2 = y - 3 - 4 = z + 1 3 , d 2 : x - 3 - 2 = y + 1 3 = z - 2 4 có phương trình là
![]()
![]()
![]()
![]()
Đáp án D
Cách giải
Vì d song song với hai mặt phẳng (P) và (Q) nên nhận
![]()
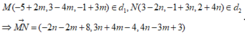

Đường thẳng d song song với hai mặt phẳng P : 3 x + 12 y - 3 z - 5 = 0 , Q : 3 x - 4 y + 9 z + 7 = 0 và đồng thời cắt cả hai đường thẳng d 1 : x + 5 2 = y - 3 - 4 = z + 1 3 , d 2 : x - 3 - 2 = y + 1 3 = z - 2 4 có phương trình là
A. x + 3 8 = y + 1 3 = z - 2 4
B. x - 3 8 = y + 1 3 = z - 2 4
C. x + 3 - 8 = y + 1 3 = z + 2 4
D. x + 3 - 8 = y + 1 3 = z - 2 4
Chọn D
Cách giải : Vì d song song với hai mặt phẳng (P) và (Q) nên nhận


Phương trình: ( z + 3 - i ) 2 - 6(z + 3 - i) + 13 = 0 có 2 nghiệm phân biệt. Khẳng định nào sau đây là đúng?
A. Trong 2 nghiệm có một nghiệm bằng 0.
B. Cả 2 nghiệm đều là số thực.
C. Cả 2 nghiệm đều là số thuần ảo.
D. Trong 2 nghiệm có 1 nghiệm là số thực, 1 nghiệm là số thuần ảo.
Dùng phương pháp bất đẳng thức để giải phương trình sau (x^2+1)(y^2+4)(z^2+9)=48xyz(x;y;z>0)
Em học lớp 6 vào chtt nha tick cho em với
gọi z1, z2 là hai nghiêm cảu phương trình z2-4Z+9=0 ; M,N lần lượt là các điểm biểu diễn z1 z2 trên mặt số phức . tính độ dài đoạn thửng M,N
giải pt ta có
\(\begin{cases}z=2+\sqrt{5i}\\z=2-\sqrt{5}i\end{cases}\)
===> 2 điểm M,N lần lượt là M( 2, \(\sqrt{5}\)) VÀ N(2,-\(\sqrt{5}\))
MN=\(\sqrt{\left(2-2\right)^2+\left(-\sqrt{5}-\sqrt{5}\right)^2}\)=2\(\sqrt{5}\)