Cho số phức z = 5 - 4i. Số phức liên hợp của z có điểm biểu diễn là.
A. (-5; 4)
B. (5; -4)
C. (5;4)
D. (-5; -4)
Cho số phức z=5-4i. Số phức liên hợp của z có điểm biểu diễn là
A. (-5;4)
B. (5;-4)
C. (5;4)
D. (-5;-4)
Cho số phức z và số phức liên hợp của nó z ¯ có điểm biểu diễn là M, M’. Số phức z(4+3i) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức |z + 4i -5|
A . 1 2
B . 2 5
C . 5 34
D . 4 13
Đáp án A
Giả sử ![]()
Ta có M(a;b) và M'(a;-b)
Khi đó ![]()
Suy ra ![]() và
và ![]()
Do 4 điểm M, N, M’, N’ tạo thành hình thang cân nhận Ox làm trục đối xứng nên 4 điểm đó lập thành hình chữ nhật
![]()

Với a = -b, ta có
![]()
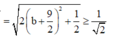
Dấu bằng xảy ra khi 
Với  ta có
ta có 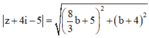
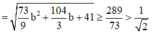
Vậy 
Cho số phức z và số phức liên hợp của nó z có điểm biểu diễn là M, M’. Số phức z . ( 4 + 3 i ) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức | z + 4 i - 5 | .
A. 1 2
B. 2 5
C. 5 34
D. 4 13
Xét số phức z và số phức liên hợp của nó có điểm biểu diễn là M và M’. Số phức z(4+3i) và số phức liên hợp của nó có điểm biểu diễn là N, N’. Biết rằng M, M’, N , N’ là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của |z+4i-5|
A . 5 34
B . 2 5
C . 1 2
D . 4 13
Đáp án C.
Giả sử ![]()
![]()
Ta có: ![]()
![]()
![]()
![]()
Để M, M’, N, N’ là 4 đỉnh của hình chữ nhật thì M phải có cùng tọa độ với N và N’
![]()
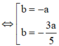
=> M nằm trên đường thẳng ![]() hoặc
hoặc ![]()
Xét điểm ![]()
![]()
Xét số phức z và số phức liên hợp của nó có điểm biểu diễn là M, M'. Số phức z(4+3i) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N'. Biết rằng M, M', N, N' là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của z + 4 i - 5 .
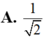
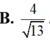
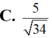
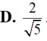
Xét số phức z và số phức liên hợp của nó có điểm biểu diễn là M và M’. Số phức z 4 + 3 i và số phức liên hợp của nó có điểm biểu diễn là N, N’. Biết rằng M, M’, N , N’ là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của z + 4 i − 5 .
A. 5 34 .
B. 2 5 .
C. 1 2 .
D. 4 13 .
Đáp án C.
Giả sử z = a + b i
với a , b ∈ ℝ ⇒ M a , b , M ' a , − b .
Ta có:
z 4 + 3 i = a + b i 4 + 3 i = 4 a − 3 b + i 4 b + 3 a ⇒ N 4 a − 3 b ; 4 b + 3 a , N ' 4 a − 3 b ; − 4 b − 3 a
Để M, M’, N, N’ là 4 đỉnh của hình chữ nhật thì M phải có cùng tọa độ với N và N’
⇔ b = ± 4 b + 3 a ⇔ b = − a b = − 3 a 5 ⇒ M nằm trên đường thẳng Δ 1 : x + y = 0 hoặc Δ 2 : 3 x + 5 y = 0
Xét điểm I 5 ; − 4 ⇒ z + 5 i − 5 = M I = M i n d I , Δ 1 , d I , Δ 1 = 1 2 .
Cho số phức z=3+4i có điểm biểu diễn là M. Số phức liên hợp của z có điểm biểu diễn là . Điểm có được bằng cách
A. tịnh tiến điểm M sang phải theo phương song song với trục hoành 4 đơn vị
B. lấy đối xứng điểm M qua gốc tọa độ
C. lấy đối xứng điểm M qua trục tung
D. lấy đối xứng điểm M qua trục hoành
Cho số phức z = 3 + 4 i có điểm biểu diễn là M. Số phức liên hợp của z có điểm biểu diễn là M′. Điểm M′ có được bằng cách
A. lấy đối xứng điểm M qua gốc tọa độ
B. lấy đối xứng điểm M qua trục tung
C. tịnh tiến điểm M sang phải theo phương song song với trục hoành 4 đơn vị
D. lấy đối xứng điểm M qua trục hoành
Đáp án D
Số phức liên hợp z ¯ = 3 − 4 i . Vậy M ' 3 ; − 4 Ta lấy điểm đối xứng với điểm M qua trục hoành.
Cho số phức z=25/(3+4i). Điểm biểu diễn hình học số phức liên hợp của z trong mặt phẳng Oxy là
A.M(3;-4)
B.N(2;-3)
C.P(3;-2)
D.Q(3;4)